练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在等边中，点，分别在边，上，且，过点作，交的延长线于点，

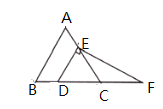
    （1）求的度数：

    （2）若，求的长.

    【答案】（1）∠F =30°；（2）DF=10．

    【解析】

    （1）根据平行线的性质可得∠EDC=∠B=60°，再根据直角三角形两锐角互余，即可求出∠F的度数；
    （2）证明△EDC是等边三角形可求得DE，再根据含30°角直角三角形的性质即可求解．

    解：（1）∵△ABC是等边三角形，
    ∴∠ACB=∠B=60°，
    ∵DE∥AB，
    ∴∠EDC=∠B=60°，
    ∵EF⊥DE，
    ∴∠DEF=90°，
    ∴∠F=90°-∠EDC=30°；
    （2）∵∠ACB=60°，∠EDC=60°，
    ∴△EDC是等边三角形．
    ∴ED=DC=5，
    ∵∠DEF=90°，∠F=30°，
    ∴DF=2DE=10．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售如下:

    每人销售件数

    1800

    510

    250

    210

    150

    120

    人数

    1

    1

    3

    5

    3

    2

    （1）求这15位营销人员该月销售量的平均数、中位数和众数.

    （2）假设销售部负责人把每位营销员的月销售额定为320件，你认为是否合理?为什么?如不合理，请你制定一个合理的销售定额，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列条件中，不能判断△ABC是直角三角形的是（　　）

    A. a：b：c＝3：4：5 B. ∠A：∠B：∠C＝3：4：5

    C. ∠A+∠B＝∠C D. a：b：c＝1：2：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A（4，3）是反比例函数y=在第一象限图象上一点，连接OA，过A作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y=的图象于点P．

    （1）求反比例函数y=的表达式；

    （2）求点B的坐标；

    （3）求△OAP的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α（0°＜α＜180°）,点B的对应点为点D,点C的对应点为点E,连接BD，BE．

    （1）如图,当α=60°时,延长BE交AD于点F．

    ①求证：△ABD是等边三角形；

    ②求证：BF⊥AD，AF=DF；

    ③请直接写出BE的长；

    （2）在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值．

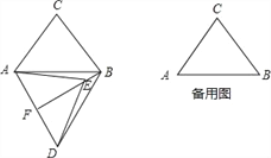
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一段圆弧与长度为1的正方形网格的交点是A、B、C．

    (1)请完成以下操作：

    ①以点O为原点，垂直和水平方向为轴，网格边长为单位长，建立平面直角坐标系；

    ②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD；

    (2)请在(1)的基础上，完成下列填空：⊙D的半径为__________；点（6，–2）在⊙D__________；（填“上”、“内”、“外”）∠ADC的度数为__________．

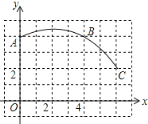
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】古代名著《算学启蒙》中有一题：“良马日行二百四十里.驽马日行一百五十里.驽马先行十二日，问良马几日追及之”，如图是两马行走的路程关于时间的函数图像.

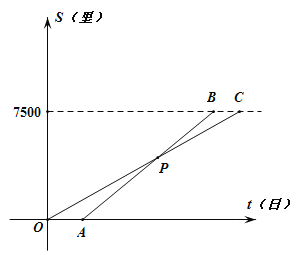
    （1）的函数解析式为_______.

    （2）求点的坐标.

    （3）若两匹马先在甲站，再从甲站出发行往乙站，并停留在乙站，且甲、乙两站之间的路程为里，请问为何值时，驽马与良马相距里？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

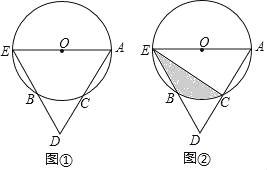
    【题目】如图①，AE是⊙O的直径，点C是⊙O上的点，连结AC并延长AC至点D，使CD=CA，连结ED交⊙O于点B．

    （1）求证：点C是劣弧的中点；

    （2）如图②，连结EC，若AE=2AC=6，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的个数（ ）

    ①近似数精确到十分位：

    ②在，，，中，最小的数是

    ③如图①所示，在数轴上点所表示的数为

    ④反证法证明命题“一个三角形中最多有一个钝角”时，首先应假设“这个三角形中有两个钝角”

    ⑤如图②，在内一点到这三条边的距离相等，则点是三个角平分线的交点

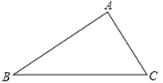
    图① 图②

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案