
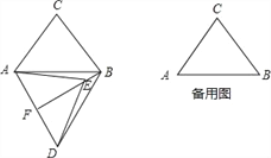
【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
【答案】(1)①②详见解析;③3![]() ﹣4;(2)13.
﹣4;(2)13.
【解析】
(1)①由旋转性质知AB=AD,∠BAD=60°即可得证;②由BA=BD、EA=ED根据中垂线性质即可得证;③分别求出BF、EF的长即可得;
(2)由∠ACB+∠BAC+∠ABC=180°、∠DAG+∠DAE+∠BAE=180°、∠DAG=∠ACB、∠DAE=∠BAC得∠BAE=∠BAC且AE=AC,根据三线合一可得CE⊥AB、AC=5、AH=3,继而知CE=2CH=8、BE=5,即可得答案.
(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AB=AD,∠BAD=60°,
∴△ABD是等边三角形;
②由①得△ABD是等边三角形,
∴AB=BD,
∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AC=AE,BC=DE,
又∵AC=BC,
∴EA=ED,
∴点B、E在AD的中垂线上,
∴BE是AD的中垂线,
∵点F在BE的延长线上,
∴BF⊥AD, AF=DF;
③由②知BF⊥AD,AF=DF,
∴AF=DF=3,
∵AE=AC=5,
∴EF=4,
∵在等边三角形ABD中,BF=ABsin∠BAF=6×![]() =3
=3![]() ,
,
∴BE=BF﹣EF=3![]() ﹣4;
﹣4;
(2)如图所示,
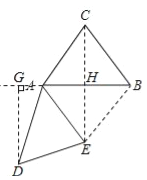
∵∠DAG=∠ACB,∠DAE=∠BAC,
∴∠ACB+∠BAC+∠ABC=∠DAG+∠DAE+∠ABC=180°,
又∵∠DAG+∠DAE+∠BAE=180°,
∴∠BAE=∠ABC,
∵AC=BC=AE,
∴∠BAC=∠ABC,
∴∠BAE=∠BAC,
∴AB⊥CE,且CH=HE=![]() CE,
CE,
∵AC=BC,
∴AH=BH=![]() AB=3,
AB=3,
则CE=2CH=8,BE=5,
∴BE+CE=13.


科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).
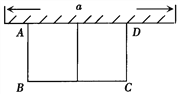
(1)如果所围成的花圃的面积为45m2,试求宽AB的长;
(2)按题目的设计要求,能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为![]() 的扇形
的扇形![]() 中,
中,![]() ,点
,点![]() 是弧
是弧![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合)
重合)![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.

![]() 当
当![]() 时,求线段
时,求线段![]() 的长;
的长;
![]() 在
在![]() 中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
![]() 设
设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
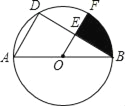
【题目】如图所示,AB是⊙O的直径,AB=4,D是⊙O上的一点,∠ABD=30°,OF∥AD交BD于点E,交⊙O于点F.
(1)求DE的长度;
(2)求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
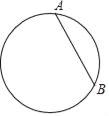
【题目】如图,已知圆上两点A,B.
(1)用直尺和圆规求作圆心(保留作图痕迹,不写画法);
(2)若AB=6,此圆的半径为2![]() ,求弦AB与劣弧AB所组成的弓形面积.
,求弦AB与劣弧AB所组成的弓形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 是高,
是高,![]() 、
、![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(变式思考)如图2,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高,若
边上的高,若![]() 的外角
的外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() ,其反向延长线与
,其反向延长线与![]() 边的延长线交于点
边的延长线交于点![]() ,则
,则![]() 与
与![]() 还相等吗?说明理由;
还相等吗?说明理由;
(探究延伸)如图3,在![]() 中,
中,![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.![]() 的外角
的外角![]() 的平分线所在直线
的平分线所在直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .直接写出
.直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
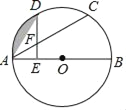
【题目】如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com