练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．若某人沿坡度i=1：3的斜坡前进20米，则他所在的位置比原来的位置高2$\sqrt{10}$米．

    分析 根据坡度是坡面的铅直高度和水平宽度的比求出$\frac{AC}{BC}$，运用方程思想和勾股定理解得即可．

    解答 解：∵斜坡的坡度i=1：3，
    ∴$\frac{AC}{BC}$=$\frac{1}{3}$，
    设AC=x，则BC=3x，
    由勾股定理得，x2+（3x）2=202，
    解得x=2$\sqrt{10}$，
    故答案为：2$\sqrt{10}$米．

    点评 本题考查的是解直角三角形的应用，掌握解直角三角形的一般步骤和坡度的概念：坡度是坡面的铅直高度h和水平宽度l的比是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．一个两位数，他的个位数与十位数的和为4，那么符合条件的两位数为（　　）
    A．3个B．4个C．5个D．无数个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．平移抛物线y=2x2所得到的函数图象经过（-1，1）及（2，3）两点．则这个图象对应的函数关系式为y=2x2-$\frac{4}{3}$x-$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．若实数α、β分别满足α2+2016α-1=0与β2+2016β-1=0，αβ不等于0；则α2β+αβ2-αβ=2017．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．已知关于x的一元二次方程x2-ax-1=0（其中a为常数）的根的情况是（　　）
    A．有两个不相等的实数根B．可能有实数根，也可能没有实数根
    C．有两个不相等的实数根D．没有实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．若x=-1是方程x-x2-k=0的一个根，则k为（　　）
    A．1B．-1C．-2D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

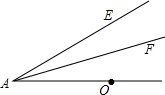    17．如图，AF平分∠OAE，M是射线AF上一动点，N是线段AO上一动点，判断是否存在点M、N．使得OM+NM的值最小？若存在，请画出M、N点，并加以说明：若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．阅读下面材料：
    点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．
    当A、B两点中有一点在原点时，不妨设点A在原点，
    如图1，|AB|=|OB|=|b|=|a-b|；
    当A、B两都不在原点时，
    如图2，点A、B都在原点的右边
    |AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
    如图3，点A、B都在原点的左边，
    |AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；
    如图4，点A、B在原点的两边，
    |AB|=|OB|+|OA|=|a|+|b|=a+（-b）=|a-b|；

    回答下列问题：
    （1）数轴上表示2和5的两点之间的距离是3，数轴上表示-2和-5的两点之间的距离是4，数轴上表示1和-3的两点之间的距离是4；
    （2）数轴上表示x和3的两点A和B之间的距离是|x-3|，如果|AB|=2，那么x为1或5；
    （3）式子|x+1|+|x-3|的最小值是4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，⊙O的半径为5cm，AB、AC是⊙O的两条弦，AB=6$\sqrt{2}$cm，AC=8cm．过点O作一个圆与AC相切，则这个圆的半径是多少？它与AB具有怎样的位置关系？为什么？

    查看答案和解析>>

    同步练习册答案