
 如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4).
如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4).| k |
| x |
| k |
| -2 |
| 8 |
| x |
| 8 |
| x |
| 8 |
| a |
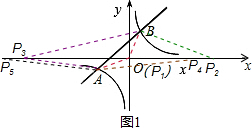 (3)存在这样的点P.理由如下:
(3)存在这样的点P.理由如下:| 2 |
| (t-2)2+42 |
| 2 |
| 14 |
| 14 |
| 14 |
| (t+4)2+22 |
| 2 |
| 17 |
| 17 |
| 17 |
| 17 |
| 17 |
| 14 |
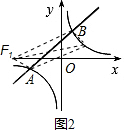 2
2| 14 |
| 8 |
| x |
| 8 |
| x |
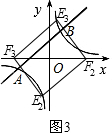 ②如图3,当以AB为平行四边形的边时,则AB∥EF且AB=EF,
②如图3,当以AB为平行四边形的边时,则AB∥EF且AB=EF,
|
|
|
| 14 |
| 3 |
| 14 |
| 3 |
| 14 |
| 3 |
| 14 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,已知一次函数与反比例函数的图象交于点P(-4,-2)和点Q(2,m)
如图,已知一次函数与反比例函数的图象交于点P(-4,-2)和点Q(2,m)查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•宁波)如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4).
(2012•宁波)如图,已知一次函数与反比例函数的图象交于点A(-4,-2)和B(a,4).查看答案和解析>>
科目:初中数学 来源: 题型:
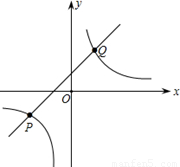
 如图,已知一次函数与反比例函数的图象交于点P(-2,-1)和点Q(1,m)
如图,已知一次函数与反比例函数的图象交于点P(-2,-1)和点Q(1,m)查看答案和解析>>
科目:初中数学 来源:2012届江苏省盐城市九年级下学期期中考试数学卷 题型:选择题
(本题满分8分)
如图,已知一次函数与反比例函数的图象交于点P(-2,-1)和点Q(1,m)
(1)求这两个函数的关系式;
(2)根据图象,直接写出当一次函数的值大于反比例函数的值时自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com