搜索
【题目】已知：如图，在
中，
，点D、E分别是AB、AC的中点，点F在BC延长线上，连接EF，且
．
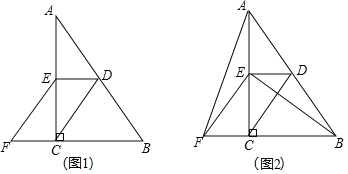
如图1，求证：四边形CDEF是平行四边形；
如图2，连接AF、BE，在不添加任何辅助线的情况下，请直接写出图2中所有与
面积相等的三角形．
参考答案：
【答案】
证明见解析； 
与
面积相等的三角形有：
，
，
，
．
【解析】
（1）根据三角形中位线性质得
，根据直角三角形斜边上中线性质得
，再证
，得
，可证四边形CDEF是平行四边形．（2）由（1）可知有关相等的线段，根据三角形的面积公式进行分析即可.
证明：
点D、E分别是AB、AC的中点，
是
的中位线，
，
，
，
，
，
，
，
，
四边形CDEF是平行四边形．
如图2中，与面积相等的三角形有：，，，．
理由：四边形CDEF是平行四边形，
与
的面积相等，
，，
与，与的面积相等，
与面积相等的三角形有：，，，．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为贯彻落实十九大会议精神，践行“绿水青山就是金山银山”的发展理念，积极推动生态文明理念融入学校教育，某中学拟举办“爱家乡、览名山”活动，围绕“哈尔滨市周边五大名山，即：香炉山、凤凰山、金龙山、帽儿山、二龙山，你最喜欢那一座山？
每名学生必选且只选一座山
”的问题在全校范围内随机抽取了部分学生进行问卷调查，根据调查结果绘制了如图所示的不完整统计图
请根据统计图的信息回答下列问题：
本次调查共抽取了多少名学生？
求本次调查中，最喜欢风凰山的学生人数，并补全条形统计图；
若该中学共有学生1200人，请你估计该中学最喜欢香炉山的学生约有多少人．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB，CD相交于点O，OA平分∠EOC．
（1）若∠EOC=70°，求∠BOD的度数；
（2）若∠EOC：∠EOD=2：3，求∠BOD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（ ）
A.7
B.8
C.9
D.10 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是半圆O的直径，C是半圆O上一点，弦AD平分∠BAC，交BC于点E，若AB=6，AD=5，则DE的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：PA是
的切线，点B在上，连接OB，OP，连接AB交OP于点C，
．
如图1，求证：
；
如图2，OP交于点D，过点D作
交AB于点E，连接OE，求证：
；
如图3，在的条件下，延长PO交于点N，连接AN交DF于点M，连接OM、EP，若
，
，求线段BE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：在平面直角坐标系xOy中，直线
分别交x、y轴于点A、C，点B在x轴负半轴上，过点A作
于点K，若
，
．
如图1，求点B坐标；
如图2，点P为AC延长线上一点，过点P作
交直线BC于点Q，设点P的横坐标为t，PQ长为d，求d与t的函数关系式
不必写出自变量t的取值范围
；
在的条件下，连接OK，过点P作
轴于点H，点F为HB上一点，连接PF，点D在PF上，将点F沿x轴正方向平移
个单位到点G，连接DG，交PH于点E，若
，
，
，求点P坐标．
相关试题
