
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF. 
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
【答案】
(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC
(2)解:四边形ADCF是菱形,
证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,
∴AD= ![]() BC=DC,
BC=DC,
∴平行四边形ADCF是菱形
【解析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案;(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.
【考点精析】本题主要考查了直角三角形斜边上的中线和菱形的判定方法的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】一列长150米的火车,以每秒15米的速度通过600米的隧道,从火车进入隧道口算起,这列火车完全通过隧道所需时间是 ( )
A.60秒
B.30秒
C.40秒
D.50秒
查看答案和解析>>
科目:初中数学 来源: 题型:
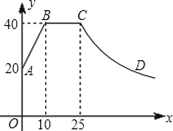
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
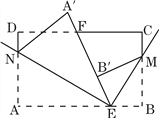
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数,并直接写出∠B′ME互余的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2017排列成如下图所示的一个数表:

(1)用一正方形在表中随意框住4个数,把其中最小的数记为![]() ,另三个数用含
,另三个数用含![]() 的式子表示出来,从大到小依次是 , , ;
的式子表示出来,从大到小依次是 , , ;
(2)当被框住的4个数之和等于416时, ![]() 的值是多少?
的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com