
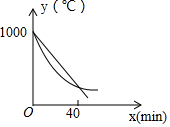
 某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过xmin时,A、B两组材料的温度分别为yA℃、yB℃;yA、yB与x的函数关系式分别为yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分图象如图所示,当x=40时,两组材料的温度相同).
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过xmin时,A、B两组材料的温度分别为yA℃、yB℃;yA、yB与x的函数关系式分别为yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分图象如图所示,当x=40时,两组材料的温度相同).分析 (1)根据题意和函数图象中的数据可以分别求得yA、yB与x的函数关系式;
(2)将y=120代入(1)中yA与x的函数关系式,然后将此时x的值再代入(1)中yB与x的函数关系式,本题得以解决;
(3)根据题意,将(1)中两个函数解析式作差,然后根据0<x<40,即可解答本题.
解答 解:(1)由函数图象可得,
当x=0时,yB=1000,
即1000=$\frac{1}{4}$(0-60)2+m,得m=100,
∴yB=$\frac{1}{4}$(x-60)2+100,
当x=40时,yB=$\frac{1}{4}$(40-60)2+100=200,
∴yA=kx+b过点(0,1000),(40,200),
∴$\left\{\begin{array}{l}{b=1000}\\{40k+b=200}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-20}\\{b=1000}\end{array}\right.$,
∴yA=-20x+1000,
即yA与x的函数关系式为yA=-20x+1000,yB与x的函数关系式为yB=$\frac{1}{4}$(x-60)2+100;
(2)将yA=120代入yA=-20x+1000得,
120=-20x+1000,得x=44,
将x=44代入yB=$\frac{1}{4}$(x-60)2+100,得
yB=$\frac{1}{4}$(44-60)2+100=164,
即当A组材料的温度降至120℃时,B组材料的温度是164℃;
(3)由题意可得,
当0<x<40时,yA-yB=-20x+1000-$\frac{1}{4}$(x-60)2-100=-$\frac{1}{4}$x2+10x=-$\frac{1}{4}$(x-20)2+100,
∴当x=20时,两组材料的温差最大,此时两组材料的温差最大为100℃.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,利用数形结合的思想和函数的思想解答本题.


科目:初中数学 来源: 题型:解答题
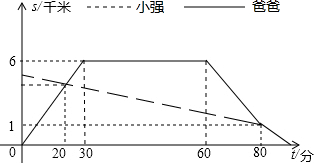 小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.
小强的爸爸从家骑自行车去图书馆借书,途中遇到了从图书馆步行回家的小强,爸爸借完书后迅速回家,途中追上了小强,便用自行车载上小强一起回家,结果爸爸比自己单独骑车回家晚到1分钟,两人与家的距离S(千米)和爸爸从家出发后的时间t(分钟)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com