

分析 直接利用同一时刻物体实际高度与影长成比例进而得出甲树的高,再利用甲树高度求法重新构造直角三角形进而得出乙树和丙树的高.
解答  解:A小组:∵一根长为1米的竹竿的影长为0.8米,甲树的影长为4米,
解:A小组:∵一根长为1米的竹竿的影长为0.8米,甲树的影长为4米,
∴甲树的高度为:$\frac{4}{0.8}$=5(m),
答:甲树的高度为5m;
B小组:如图①,过点D作DM⊥AB于点M,
由题意可得:$\frac{1}{0.8}$=$\frac{BM}{2.4}$,
解得:BM=3,
故乙树的高度为:3+1.2=4.2(m),
答:乙树的高度为4.2m;
C小组:如图②,连接PR,延长OQ,交PR于点H,作MR⊥OP于M,
过点Q作QN⊥MR于点N,
由题意可得:OH为OP的影长,
则$\frac{OP}{OH}$=$\frac{1}{0.8}$,
∵∠OQR=150°,
∴∠1=30°,
则∠2=∠1=30°,
∴QN=$\frac{1}{2}$QR=2m,
∴RN=2$\sqrt{3}$m,∴RM=2+2$\sqrt{3}$(m),
∵OH∥RM,
∴△POH∽△PMR,
∴$\frac{PO}{OH}$=$\frac{PM}{MR}$,
∴$\frac{PM}{MR}$=$\frac{1}{0.8}$,
∴PM=$\frac{5+5\sqrt{3}}{2}$,
∴OP=$\frac{5+5\sqrt{3}}{2}$-2=$\frac{1+5\sqrt{3}}{2}$(m),
答:丙树的高为:$\frac{1+5\sqrt{3}}{2}$m.
点评 此题主要考查了相似三角形的应用以及锐角三角函数关系,正确构造直角三角形是解题关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
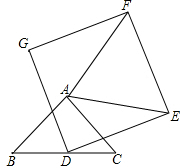 如图,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,连接AE,若BC=DE=2,将正方形DEFG绕点D逆时针方向旋转,在旋转过程中,当AE为最大值时,求AF的值.
如图,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,连接AE,若BC=DE=2,将正方形DEFG绕点D逆时针方向旋转,在旋转过程中,当AE为最大值时,求AF的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该校六年级全体学生 | |
| B. | 随机抽取的100名六年级学生 | |
| C. | 该校六年级全体学生的体能情况 | |
| D. | 随机抽取的100名六年级学生的体能情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com