
【题目】如图,抛物线 y=﹣![]() x2+
x2+![]() x+2 与 x 轴交于点 A,B,与 y 轴交于点C.
x+2 与 x 轴交于点 A,B,与 y 轴交于点C.
(1)求 A,B,C的坐标;
(2)直线 l:y=﹣![]() x+2上有一点 D(m,﹣2),在图中画出直线 l和点 D,并判断四边形ACBD的形状,说明理由.
x+2上有一点 D(m,﹣2),在图中画出直线 l和点 D,并判断四边形ACBD的形状,说明理由.
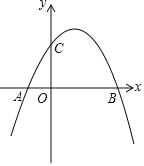
【答案】(1)A(﹣1,0);B(4,0);C(0,2);(2)图形见解析;四边形ACBD为矩形.
【解析】
(1)分别代入x=0,y=0求出与之对应的y,x的值,进而即可得出点A,B,C的坐标;
(2)利用一次函数图象上点的坐标特征可求出点D的坐标,依照题意画出图形,设CD交AB于点E,利用一次函数图象上点的坐标特征可求出点E的坐标,结合点A,B,C的坐标可得出AB=CD,AB,CD互相平分,利用矩形的判定定理即可证出四边形ACBD为矩形.
(1)当x=0时,y![]() x2
x2![]() x+2=2,∴点C的坐标为(0,2).
x+2=2,∴点C的坐标为(0,2).
当y=0时,有![]() x2
x2![]() x+2=0,解得:x1=﹣1,x2=4,∴点A的坐标为(﹣1,0),点B的坐标为(4,0).
x+2=0,解得:x1=﹣1,x2=4,∴点A的坐标为(﹣1,0),点B的坐标为(4,0).
(2)∵点D(m,﹣2)在直线y![]() x+2上的,∴﹣2
x+2上的,∴﹣2![]() m+2,解得:m=3,∴点D的坐标为(3,﹣2).
m+2,解得:m=3,∴点D的坐标为(3,﹣2).
依照题意画出图形,设CD交AB于点E,如图所示,四边形ACBD为矩形.理由如下:
当y=0时,有![]() x+2=0,解得:x
x+2=0,解得:x![]() ,∴点E的坐标为(
,∴点E的坐标为(![]() ,0).
,0).
∵A(﹣1,0),B(4,0),C(0,2),D(3,﹣2),E(![]() ,0),∴AB=4﹣(﹣1)=5,CD
,0),∴AB=4﹣(﹣1)=5,CD![]() 5,CE
5,CE![]() ,AE
,AE![]() (﹣1)
(﹣1)![]() ,∴AE
,∴AE![]() AB,CE
AB,CE![]() CD,∴AB=CD,AB,CD互相平分,∴四边形ACBD为矩形.
CD,∴AB=CD,AB,CD互相平分,∴四边形ACBD为矩形.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB交双曲线 ![]() 于A,B两点,交x轴于点C,且BC=
于A,B两点,交x轴于点C,且BC= ![]() AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=6,求图中阴影部分的面积(结果保留根号和π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)在这个问题中,总体指的是?个体指的是?样本是?样本容量是?
(2)试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4 经过点A(﹣3,0),点 B 在抛物线上,CB∥x轴,且AB 平分∠CAO.则此抛物线的解析式是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
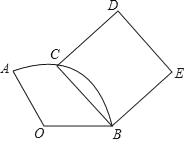
【题目】如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在![]() 上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
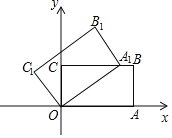
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票。王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为 偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动。你认为这个方法公平吗?请画树状图或列表,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com