
【题目】已知抛物线![]() 的图象与
的图象与![]() 轴有两个公共点.
轴有两个公共点.
(1)求![]() 的取值范围,写出当
的取值范围,写出当![]() 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为![]() ,
,
①求![]() 的顶点
的顶点![]() 的坐标;
的坐标;
②若当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的值;
的值;
(3)将![]() 平移得到抛物线
平移得到抛物线![]() ,使
,使![]() 的顶点
的顶点![]() 落在以原点为圆心半径为
落在以原点为圆心半径为![]() 的圆上,求点
的圆上,求点![]() 与
与![]() 两点间的距离最大时
两点间的距离最大时![]() 的解析式,怎样平移
的解析式,怎样平移![]() 可以得到所求抛物线?
可以得到所求抛物线?

【答案】(1)![]() ;(2) ①
;(2) ①![]() ,②1;(3)
,②1;(3)![]() 的解析式为
的解析式为![]() .将抛物线记为
.将抛物线记为![]() 向左平移
向左平移![]() ,再向上平移
,再向上平移![]() 即可得到抛物线
即可得到抛物线![]() .
.
【解析】试题分析:(1)函数图形与x轴有两个公共点,则该函数为二次函数且△>0,故此可得到关于m的不等式组,从而可求得m的取值范围;
(2)①把(1)中求得的函数解析式改为顶点式,即可得出顶点P的坐标;
②先求得抛物线的对称轴,当1≤x≤n时,函数图象位于对称轴的右侧,y随x的增大而增大,当x=n时,y有最大值2n,然后将x=n,y=2n代入求解即可;
(3)由弦的性质可得当PQ经过圆心时,PQ有最大值,此时Q点位于第二象限.根据点P、O的坐标,求得直线OP的解析式,设出点Q的坐标,根据点Q在直线PO上,以及点Q到原点的距离是![]() 即可求出点Q的坐标,进而得出C2的解析式,得出C2如何由C1平移得到.
即可求出点Q的坐标,进而得出C2的解析式,得出C2如何由C1平移得到.
试题解析:
解:(1)由题意可得: 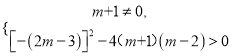 ,
,
解得: ![]() 且
且![]()
当![]() 取最大整数时,其值为2,此时函数解析式为:
取最大整数时,其值为2,此时函数解析式为: ![]() .
.
(2)①由![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
②抛物线C1的对称轴为![]() ,
,
∴当![]() 时,
时, ![]() 随
随![]() 的增大而增大.
的增大而增大.
∵当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
(3)由弦的性质,当线段![]() 经过圆心
经过圆心![]() 时,
时, ![]() 距离最大,此时点
距离最大,此时点![]() 位于第二象限.
位于第二象限.
由![]() ,
, ![]() 可求得直线
可求得直线![]() 的解析式为:
的解析式为: ![]() ,
,
设![]() ,PQ在直线
,PQ在直线![]() 上,
上, ![]() ,
,
圆![]() 半径为
半径为![]() ,
, ![]() ,
,
解之得![]() (舍去)或者
(舍去)或者![]() ,故
,故![]() .
.
∴![]() 的解析式为:
的解析式为: ![]() .
.
将抛物线记为![]() 向左平移
向左平移![]() 再向上平移
再向上平移![]() 即可得到抛物线记为
即可得到抛物线记为![]() .
.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.
⑴求这条直线的函数关系式及点![]() 的坐标 ;
的坐标 ;
⑵在![]() 轴上是否存在点
轴上是否存在点![]() ,使得△
,使得△![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
⑶过线段![]() 上一点
上一点![]() ,作
,作![]() ∥
∥![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限;点
在第一象限;点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时, ![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线
与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线![]() .
.
(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;
(2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线![]() 的对称点为N,试证明四边形CDAN是平行四边形;
的对称点为N,试证明四边形CDAN是平行四边形;
(3)点P在直线![]() 上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.
上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )
x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 地出发,匀速驶向
地出发,匀速驶向![]() 地.甲车以
地.甲车以![]() 的速度行驶
的速度行驶![]() 后,乙车才沿相同路线行驶.乙车先到达
后,乙车才沿相同路线行驶.乙车先到达![]() 地并停留
地并停留![]() 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离
后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离![]() 与乙车行驶时间
与乙车行驶时间![]() 之间的函数关系如图所示.下列说法:①乙车的速度是
之间的函数关系如图所示.下列说法:①乙车的速度是![]() ;②
;②![]() ;③点
;③点![]() 的坐标是
的坐标是![]() ;④
;④![]() .其中说法正确的是_________.
.其中说法正确的是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国庆”期间,某电影院装修后重新开业,试营业期间统计发现,影院每天售出的电影票张数y(张)与电影票售价![]() (元/张)之间满足一次函数关系:
(元/张)之间满足一次函数关系: ![]() ,
, ![]() 是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入
是整数,影院每天运营成本为1600元,设影院每天的利润为w(元)(利润=票房收入![]() 运营成本).
运营成本).
(1)试求w与![]() 之间的函数关系式;
之间的函数关系式;
(2)影院将电影票售价定为多少时,每天获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF//BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.
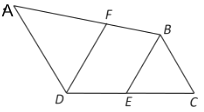
解: 因为DF平分∠CDA,(已知)
所以∠FDC=![]() ∠_________.(____________________)
∠_________.(____________________)
因为∠CDA=120°,(已知)所以∠FDC=______°.
因为DF//BE,(已知)
所以∠FDC=∠_________=60°.(____________________________________)
又因为EC=EB,(已知)
所以△BCE为等边三角形.(________________________________________)
因为△BCE的周长为18cm,(已知) 所以BE=EC=BC=6 cm.
因为点E是DC的中点,(已知) 所以DC=2EC=12 cm .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从我市至枣庄正在修筑的高速公路经过某村,需把本村部分农户搬迁至一个规划区域建房.若这批搬迁农户建房每户占地![]() ,则规划区域内绿地面积占规划区域总面积的
,则规划区域内绿地面积占规划区域总面积的![]() ;政府又鼓励本村不需要搬迁的农户到规划区域建房,这样又有
;政府又鼓励本村不需要搬迁的农户到规划区域建房,这样又有![]() 户农户加入建房,若仍以每户占地
户农户加入建房,若仍以每户占地![]() 计算,则这时绿地面积只占规划区域总面积的
计算,则这时绿地面积只占规划区域总面积的![]() .问:
.问:
(1)(列方程组解应用题)最初必须搬迁建房的农户有多少,政府的规划区域总面积是多少平方米?
(2)若要求绿地面积不得少于规划区域总面积的![]() ,为了符合要求,需要退出部分农户,至少需要退出几户农户?
,为了符合要求,需要退出部分农户,至少需要退出几户农户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com