
【题目】如图,已知在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线
与x轴交于点A(﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线![]() .
.
(1)求这条抛物线的关系式,并写出其对称轴和顶点M的坐标;
(2)如果直线y=kx+b经过C、M两点,且与x轴交于点D,点C关于直线![]() 的对称点为N,试证明四边形CDAN是平行四边形;
的对称点为N,试证明四边形CDAN是平行四边形;
(3)点P在直线![]() 上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.
上,且以点P为圆心的圆经过A、B两点,并且与直线CD相切,求点P的坐标.

【答案】(1)∴y=﹣x2+2x+3,对称轴为直线x=1,顶点M(1,4);(2)证明见解析; (3)P1(1,﹣4+2![]() ),P2(1,﹣4﹣2
),P2(1,﹣4﹣2![]() ).
).
【解析】试题分析:(1)将A、C两点坐标代入解析式即可求出![]() ,将解析式配成顶点式即可得到对称轴方程和顶点坐标;
,将解析式配成顶点式即可得到对称轴方程和顶点坐标;
(2)先由C、M两点坐标求出直线CM解析式,进而求出D点坐标,由于C、N两点关于抛物线对称轴对称,则CN∥AD,同时可求出N点坐标,然后得出CN=AD,结论显然;
(3)设出P点纵坐标,表示出MP的长度,过点P作![]() 于H,表示出PH的长度,在Rt△APE中中用勾股定理列出方程,解之即得答案.
于H,表示出PH的长度,在Rt△APE中中用勾股定理列出方程,解之即得答案.
试题解析:(1)∵抛物线![]() 经过点A(1,0)和点C(0,3),
经过点A(1,0)和点C(0,3),
![]()
![]()
![]()
对称轴为直线x=1,顶点M(1,4);
(2)如图1,
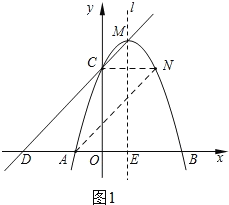
∵点C关于直线l的对称点为N,
∴N(2,3),
∵直线y=kx+b经过C.M两点,
∴![]()
∴![]()
∴y=x+3,
∵y=x+3与x轴交于点D,
∴D(3,0),
∴AD=2=CN
又∵AD![]() CN,
CN,
∴CDAN是平行四边形;
(3)设P(1,a),过点P作PH⊥DM于H,连接PA、PB,如图2,
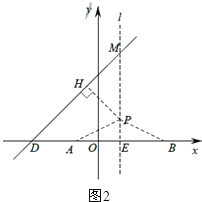
则MP=4a,
又![]()
![]()
Rt△APE中, ![]()
![]()


科目:初中数学 来源: 题型:
【题目】快递公司准备购买机器人来代替人工分拣已知购买- 台甲型机器人比购买-台乙型机器人多![]() 万元;购买
万元;购买![]() 台甲型机器人和
台甲型机器人和![]() 台乙型机器人共需
台乙型机器人共需![]() 万元.
万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型、乙型机器人每台每小时分拣快递分别是![]() 件、
件、![]() 件,该公司计划最多用
件,该公司计划最多用![]() 万元购买
万元购买![]() 台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
台这两种型号的机器人.该公司该如何购买,才能使得每小时的分拣量最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
﹣5,|-![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]()
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它们的相关函数为y= .
.
(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;
(2)已知二次函数y=﹣x2+4x﹣![]() .
.
①当点B(m, ![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当﹣3≤x≤3时,求函数y=﹣x2+4x﹣![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有A、B两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室阅读.
(1)下列事件中,是必然事件的为( )
A.甲、乙同学都在A阅览室 B.甲、乙、丙同学中至少两人在A阅览室
C.甲、乙同学在同一阅览室 D.甲、乙、丙同学中至少两人在同一阅览室
(2)用画树状图的方法求甲、乙、丙三名学生在同一阅览室阅读的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往青岛,这列货车可挂A,B两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A,B两种货厢的节数,有哪几种运输方案?请设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的图象与
的图象与![]() 轴有两个公共点.
轴有两个公共点.
(1)求![]() 的取值范围,写出当
的取值范围,写出当![]() 取其范围内最大整数时抛物线的解析式;
取其范围内最大整数时抛物线的解析式;
(2)将(1)中所求得的抛物线记为![]() ,
,
①求![]() 的顶点
的顶点![]() 的坐标;
的坐标;
②若当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的值;
的值;
(3)将![]() 平移得到抛物线
平移得到抛物线![]() ,使
,使![]() 的顶点
的顶点![]() 落在以原点为圆心半径为
落在以原点为圆心半径为![]() 的圆上,求点
的圆上,求点![]() 与
与![]() 两点间的距离最大时
两点间的距离最大时![]() 的解析式,怎样平移
的解析式,怎样平移![]() 可以得到所求抛物线?
可以得到所求抛物线?

查看答案和解析>>
科目:初中数学 来源: 题型:
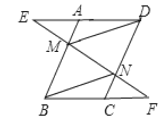
【题目】已知,如图,在平行四边形ABCD中,点M,N分别在边AB,DC上,作直线MN,分别交DA和BC的延长线于点E、F,且AE=CF.
(1) 求证:△AEM≌△CFN.
(2) 求证:四边形BNDM是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com