练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

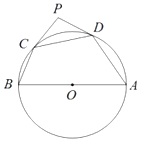
    【题目】如图，是的直径，、为上的点，为圆外一点，、均与圆相切，设，，则与满足的关系式为（ ）

    A.B.C.D.以上都不对

    【答案】B

    【解析】

    连结OC，OD，则∠PCO=90°，∠PDO=90°，可得∠CPD+∠COD=180°，根据OB=OC，OD=OA，可得∠BOC=180°-2∠B，∠AOD=180°-2∠A，则可得出α与β的关系式．

    连结OC，OD，

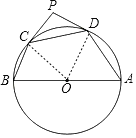
    ∵PC、PD均与圆相切，

    ∴∠PCO=90°，∠PDO=90°，

    ∵∠PCO+∠COD+∠ODP+∠CPD=360°，

    ∴∠CPD+∠COD=180°，

    ∵OB=OC，OD=OA，

    ∴∠BOC=180°-2∠B，∠AOD=180°-2∠A，

    ∴∠COD+∠BOC+∠AOD=180°，

    ∴180°-∠CPD+180°-2∠B+180°-2∠A=180°．

    ∴．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB=BC=1，则下列结论：

    ①∠CAD=30°②BD=③S平行四边形ABCD=ABAC④OE=AD⑤S△APO=，正确的个数是（　　）

    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，M是AB的中点，动点P从点A出发，

    沿AC方向匀速运动到终点C,动点Q从点C出发，沿CB方向匀速运动到终点B.已知P，Q两点同时出发，并同时到达终点.连结MP，MQ，PQ.在整个运动过程中，△MPQ的面积大小变化情况是【 】

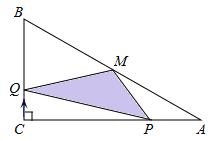
    A.一直增大 B.一直减小 C.先减小后增大 D.先增大后减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：

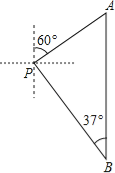
    【题目】小亮一家在一湖泊中游玩，湖泊中有一孤岛，妈妈在孤岛P处观看小亮与爸爸在湖中划船（如图所示）．小船从P处出发，沿北偏东60°方向划行200米到A处，接着向正南方向划行一段时间到B处．在B处小亮观测到妈妈所在的P处在北偏西37°的方向上，这时小亮与妈妈相距多少米（精确到1米）？

    （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，≈1.41，≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“校园安全”受到全社会的广泛关注，东营市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图中所提供的信息解答下列问题：

    （1）接受问卷调查的学生共有_______人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°；

    （2）请补全条形统计图；

    （3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；

    （4）若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

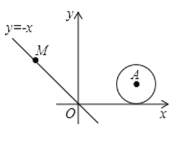
    【题目】如图，在平面直角坐标系中，⊙A的半径为1，圆心A点的坐标为（2，1）．直线OM是一次函数y=－x的图象．将直线OM沿x轴正方向平行移动．

    （1）填空：直线OM与x轴所夹的锐角度数为 °；

    （2）求出运动过程中⊙A与直线OM相切时的直线OM的函数关系式；（可直接用（1）中的结论）

    （3）运动过程中，当⊙A与直线OM相交所得的弦对的圆心角为90°时，直线OM的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

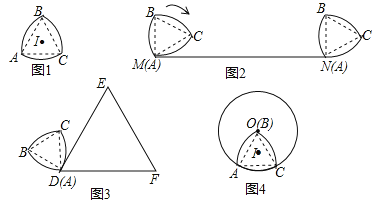
    【题目】如图1，等边△ABC的边长为3，分别以顶点B、A、C为圆心，BA长为半径作、、，我们把这三条弧所组成的图形称作莱洛三角形，显然莱洛三角形仍然是轴对称图形，设点l为对称轴的交点．

    （1）如图2，将这个图形的顶点A与线段MN作无滑动的滚动，当它滚动一周后点A与端点N重合，则线段MN的长为 ；

    （2）如图3，将这个图形的顶点A与等边△DEF的顶点D重合，且AB⊥DE，DE=2π，将它沿等边△DEF的边作无滑动的滚动当它第一次回到起始位置时，求这个图形在运动过程中所扫过的区域的面积；

    （3）如图4，将这个图形的顶点B与⊙O的圆心O重合，⊙O的半径为3，将它沿⊙O的圆周作无滑动的滚动，当它第n次回到起始位置时，点I所经过的路径长为 （请用含n的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某排球队6名场上队员的身高（单位：cm）是：180，182，184，186，190，194．现用一名身高为188cm的队员换下场上身高为182cm的队员，与换人前相比，场上队员的身高

    A.平均数变小，方差变小B.平均数变小，方差变大

    C.平均数变大，方差变小D.平均数变大，方差变大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BD⊥AC于D，CE⊥AB于E。

    （1）求证：△ABD∽△ACE

    （2）连接DE，求证：∠ADE＝∠ABC

    查看答案和解析>>

    同步练习册答案