
已知二次函数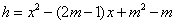 (
( 是常数,且
是常数,且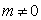 ).
).
(1)证明:不论m取何值时,该二次函数图象总与 轴有两个交点;
轴有两个交点;
 (2)若A
(2)若A 、B
、B 是该二次函数图象上的两个不同点,求二次函数解析式和
是该二次函数图象上的两个不同点,求二次函数解析式和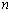 的值;
的值;
(3)设二次函数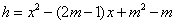 与
与 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为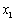 ,
,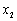 (其中
(其中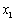 >
>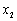 ),若
),若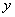 是关于
是关于 的函数,且
的函数,且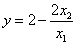 ,请结合函数的图象回答:当
,请结合函数的图象回答:当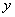 <
< 时,求m的取值范围.
时,求m的取值范围.
(1)证明:在二次函数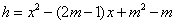 中,△=1>0,
中,△=1>0,
所以不论m取何值时,该二次函数图象总与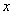 轴有两个交点. …………2分
轴有两个交点. …………2分
(2)由点A 与点B
与点B 的坐标可知二次函数的对称轴为
的坐标可知二次函数的对称轴为
直线 ,由二次函数的解析式可知对称轴为
,由二次函数的解析式可知对称轴为
直线 ,所以
,所以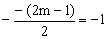 ,得
,得 ,
,
可知函数解析式为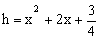 ,将
,将 带入函数解析式得
带入函数解析式得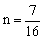 .
.
∴二次函数解析式为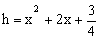 ,
,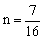 . …………4分
. …………4分
(3)由二次函数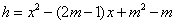 分解因式
分解因式 可得
可得 ,
,
即图像与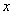 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为 ,
, (其中
(其中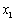 >
>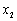 ),(也可以用求根公式求得方程的两根)
),(也可以用求根公式求得方程的两根)
∵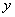 是关于
是关于 的函数,且
的函数,且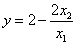 ,
,
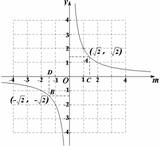 ∴
∴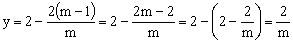 (其中
(其中 是常数,且
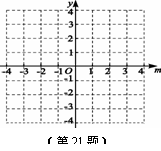
是常数,且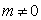 )作出此函数的图象如图,当y=m时有
)作出此函数的图象如图,当y=m时有 ,解得
,解得 ,从图
,从图 上可以看出在 垂线AC的右侧和垂线BD与x轴之间时有
上可以看出在 垂线AC的右侧和垂线BD与x轴之间时有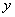 <m,所以当
<m,所以当 时有
时有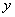 <m.
<m.
…………4分


科目:初中数学 来源: 题型:
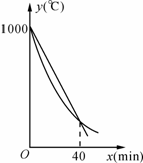
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比 实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=
实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=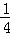 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大 ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图抛物线 与
与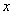 轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两个点),定点C是矩形DEFG上(包括边界和内部)的一个动点,则:
轴的一个交点A在点(-2,0)和(-1,0)之间(包括这两个点),定点C是矩形DEFG上(包括边界和内部)的一个动点,则:
(1)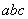 0(填
0(填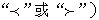
(2) 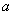 的取值范围是 。
的取值范围是 。
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,P点关于原点的对称点为
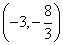 ,P点关于
,P点关于 轴的对称点为
轴的对称点为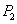
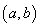 ,则
,则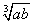 =…………………………………………………( )
=…………………………………………………( )
A.-2; B.2; C.4; D.-4;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com