
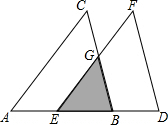
 如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{4}{9}$,若AB=2,求△ABC移动的距离BE的长.
如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{4}{9}$,若AB=2,求△ABC移动的距离BE的长. 分析 根据平移的性质得到EF∥AC,证得△BEG∽△BAC,由相似三角形的性质得到$\frac{BE}{AB}$=$\sqrt{\frac{{S}_{△BEG}}{{S}_{△ABC}}}$=$\frac{2}{3}$,即可得到结论.
解答  解:∵把△ABC沿边BA平移到△DEF的位置,
解:∵把△ABC沿边BA平移到△DEF的位置,
∴EF∥AC,
∴△BEG∽△BAC,
∴$\frac{BE}{AB}$=$\sqrt{\frac{{S}_{△BEG}}{{S}_{△ABC}}}$=$\frac{2}{3}$,
∵AB=2,
∴BE=$\frac{4}{3}$.
点评 本题主要考查相似三角形的判定和性质、平移的性质,关键在于求证△ABC与阴影部分为相似三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
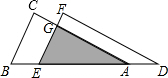 如图,△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{9}$,若AB=2,求△ABC移动的距离BE的长.
如图,△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{9}$,若AB=2,求△ABC移动的距离BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com