
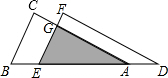
 如图,△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{9}$,若AB=2,求△ABC移动的距离BE的长.
如图,△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{9}$,若AB=2,求△ABC移动的距离BE的长. 分析 根据平移的性质得到BC∥EF,证得△AGE∽△ABC,根据相似三角形的性质得到$\frac{AE}{AB}=\sqrt{\frac{{S}_{△AGE}}{{S}_{△ABC}}}$=$\frac{1}{3}$,即可得到结论.
解答 解:∵ △ABC沿边BA平移到△DEF的位置,
△ABC沿边BA平移到△DEF的位置,
∴BC∥EF,
∴△AGE∽△ABC,
∴$\frac{AE}{AB}=\sqrt{\frac{{S}_{△AGE}}{{S}_{△ABC}}}$=$\frac{1}{3}$,
∵AB=2,
∴AE=$\frac{2}{3}$,
∴BE=$\frac{4}{3}$.
点评 本题主要考查相似三角形的判定和性质、平移的性质,关键在于求证△ABC与阴影部分为相似三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
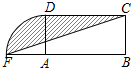 一商标图案如图阴影部分,长方形ABCD中AB=4cm,BC=2cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积为(2+π)cm2.(结果保留π)
一商标图案如图阴影部分,长方形ABCD中AB=4cm,BC=2cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积为(2+π)cm2.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
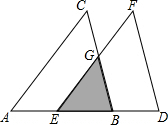 如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{4}{9}$,若AB=2,求△ABC移动的距离BE的长.
如图,把△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{4}{9}$,若AB=2,求△ABC移动的距离BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
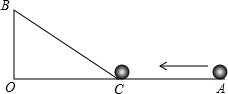 如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com