
【题目】阅读材料,解答问题.
利用图象法解一元二次不等式:x2-2x-3>0.
解:设y=x2-2x-3,则y是x的二次函数.∵a=1>0,∴抛物线开口向上.
又∵当y=0时,x2-2x-3=0,解得x1=-1,x2=3.
∴由此得抛物线y=x2-2x-3的大致图象如图所示.
观察函数图象可知:当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是:x<-1或x>3.
(1)观察图象,直接写出一元二次不等式:x2-2x-3<0的解集是 ;
(2)仿照上例,用图象法解一元二次不等式:x2-1>0.(大致图象画在答题卡上)

【答案】(1)-1<x<3;(2)x<-1或x>1.
【解析】试题分析:(1)由x2-2x-3=0得x1=-1,x2=3,抛物线y=x2-2x-3开口向上,y<0时,图象在x轴的下方,此时-1<x<3;
(2)仿照(1)的方法,解出图象与x轴的交点坐标,根据图象的开口方向及函数值的符号,确定x的范围.
试题解析:(1)-1<x<3;
(2)设y=x2-1,则y是x的二次函数,
∵a=1>0,
∴抛物线开口向上.
又∵当y=0时,x2-1=0,
解得x1=-1,x2=1.
∴由此得抛物线y=x2-1的大致图象如图所示.
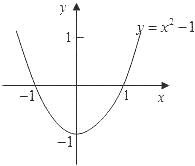
观察函数图象可知:当x<-1或x>1时,y>0.
∴x2-1>0的解集是:x<-1或x>1.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx﹣3且y随x的增大而增大,那么它的图象经过( )
A. 第二、三、四象限B. 第一、二、三象限
C. 第一、三、四象限D. 第一、二、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了应用乘法公式计算(x-2y+1)(x+2y-1),下列变形中正确的是 ( )
A. [x-(2y+1)]2 B. [x-(2y-1)][x+(2y-1)]
C. [(x-2y)+1][(x-2y)-1] D. [x+(2y-1)]2
查看答案和解析>>
科目:初中数学 来源: 题型:
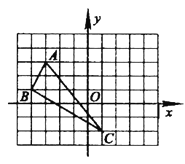
【题目】在平面直角坐标系中, 三角形ABC三个顶点的位置如图(每个小正方形的边长均为1).把三角形ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后得到三角形A′B′C′(其中A′、B′、C′分别是A、B、C的对应点.)
(1)直接写出A′、B′、C′三点的坐标:A′(____,____);B′(____,____);C′(____,____).
(2)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学书法兴趣小组10名成员的年龄情况如下表,则该小组成员年龄的众数和中位数分别是( )
年龄/岁 | 14 | 15 | 16 | 17 |
人数 | 3 | 4 | 2 | 1 |
A. 15,15B. 16,15C. 15,17D. 14,15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一学员在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来的方向相同,这两次拐弯的角度可能是( )
A. 第一次向右拐50°第二次向左拐130° B. 第一次向左拐30°第二次向右拐30°
C. 第一次向右拐50°第二次向右拐130° D. 第一次向左拐50°第二次向左拐130°
查看答案和解析>>
科目:初中数学 来源: 题型:
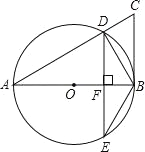
【题目】已知,如图,BC是以线段AB为直径的⊙O的切线,AC交⊙O于点D,过点D作弦DE⊥AB,垂足为点F,连接BD、BE.
(1)仔细观察图形并写出四个不同的正确结论:① ,② ,③ ,④ (不添加其它字母和辅助线,不必证明);
(2)∠A=30°,CD=![]() ,求⊙O的半径r.
,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
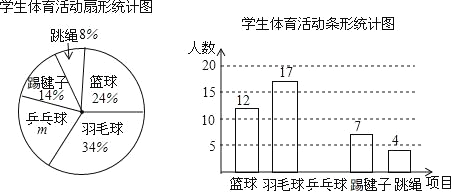
(1)m= %,这次共抽取了 名学生进行调查;并补全条形图;
(2)请你估计该校约有 名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com