
【题目】【定义】配方法是指将一个式子或一个式子的某一部分通过恒等变形华为完全平方式或几个完全平方式的和,这种方法称之为配方法.例如:可将多项式![]() 通过恒等变形化为
通过恒等变形化为![]() 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.
【理解】对于多项式![]() ,当
,当![]() = 时,它的最小值为 .
= 时,它的最小值为 .
【应用】若![]() ,求
,求![]() 的值.
的值.
【拓展】![]() 、
、![]() 、
、![]() 是△
是△![]() 的三边,且有
的三边,且有![]() .
.
(1)若![]() 为整数,求
为整数,求![]() 的值.
的值.
(2)若△![]() 是等腰三角形,直接写出这个三角形的周长.
是等腰三角形,直接写出这个三角形的周长.
【答案】【理解】![]() ,
, ![]() ;【应用】
;【应用】![]() ;【拓展】(1)c的值为4,5,6;(2)12.
;【拓展】(1)c的值为4,5,6;(2)12.
【解析】【试题分析】
【理解】![]() =
=![]() ,得当
,得当![]() =2时,它的最小值为1.
=2时,它的最小值为1.
【应用】![]() ,
,
变形得: ![]() .
.
配方得: ![]() . 则
. 则![]() ,
, ![]() .解得
.解得![]() ,
, ![]() .
.
则![]() .
.
【拓展】
(1)![]() ,
, ![]() .
.
配方得: ![]() .则
.则![]() ,
, ![]() .
.
解得![]() ,
, ![]() .
.
根据三角形两边之和大于第三边,两边之差小于第三边得: ![]() .
.
因为![]() 为整数,则
为整数,则![]() 的值为4,5,6
的值为4,5,6
(2)2,2,5(舍去)与5,5,2两种情况,得:等腰三角形的周长为12.
【试题解析】
【理解】![]()
![]()
【应用】∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,
, ![]() .
.
解得![]() ,
, ![]() .
.
∴![]() .
.
【拓展】(1)∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() ,
, ![]() .
.
解得![]() ,
, ![]() .
.
∴![]() .
.
∵![]() 为整数,
为整数,
∴![]() 的值为4,5,6.
的值为4,5,6.
(2)2,2,5(舍去)与5,5,2两种情况,得:等腰三角形的周长为12.


科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点P是⊙O上不与A,B重合的一个动点,延长PA到C,使AC=AP,点D为⊙O上一点,且满足AD∥PB,射线CD交PB延长线于点E.
(1)求证:△PAB≌△ACD;
(2)填空:
①若AB=6,则四边形ABED的最大面积为 ;
②若射线CD与⊙O的另一个交点为F,则当∠PAB的度数为 时,以O,A,D,F为顶点的四边形为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月份某省农产品实现出口额8 3620000美元.其中8 3620000用科学记数法表示为( )
A.8.362×107
B.83.62×106
C.0.8362×108
D.8.362×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角从标系中,A点坐标为(0,4),B点坐标为(2,0),C(m,6)为反比例函数y=![]() 图象上一点.将△AOB绕B点旋转至△A′O′B处.
图象上一点.将△AOB绕B点旋转至△A′O′B处.
(1)求m的值;
(2)若O′落在OC上,连接AA′交OC与D点.①求证:四边形ACA′O′为平行四边形; ②求CD的长度;
(3)直接写出当AO′最短和最长时A′点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?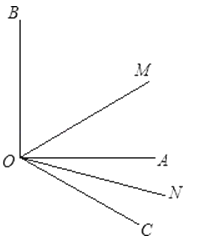
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com