
【题目】已知:如图,AB为⊙O的直径,点P是⊙O上不与A,B重合的一个动点,延长PA到C,使AC=AP,点D为⊙O上一点,且满足AD∥PB,射线CD交PB延长线于点E.
(1)求证:△PAB≌△ACD;
(2)填空:
①若AB=6,则四边形ABED的最大面积为 ;
②若射线CD与⊙O的另一个交点为F,则当∠PAB的度数为 时,以O,A,D,F为顶点的四边形为菱形.

【答案】(1)证明详见解析;(2)①18;②30°.
【解析】
试题分析:(1)连接BD,先判断出四边形ADBP矩形,得出AD=PB,再用SAS得出△PAB≌△ACD;
(2)①先判断出四边形ADEB是平行四边形,而AB是定值,要四边形ADEB面积最大,只有点D到AB的距离最大,最大为圆的半径,最后根据三角形面积公式计算即可;
②要使四边形OADF是菱形,即OA=AD,得出三角形AOD是等边三角形,即∠OAD=60°即可.
试题解析:(1)如图1,连接,BD,
∵AB为⊙O的直径,
∴∠APB=∠ADB=90°,
∵AD∥PB,
∴∠CAD=∠APB=90°,
∴∠PAD=90°
∴∠APB=∠ADB=∠PAD=90°,
∴四边形ADBP是矩形,
∴AD=PB,
在△PAB≌和△ACD中,
AC=AP,∠CAD=∠APB,AD=PB,
∴△PAB≌△ACD;

(2)①由(1)知,AD=PB
∵AD∥PB,AC=AP,
∴AD=![]() PE=
PE=![]() (PB+BE),
(PB+BE),
∴PB=EB,
∴AD=BE,
∵AD∥PB,
∴四边形ADEB是平行四边形,
∵AB是⊙O的直径,不变,
∴直线CD和⊙O相切时,即:点D到直径AB的等于半径时,四边形ABED的最大,
∵AB=6
∴S四边形ABED的最大=AB×![]() AB=18,
AB=18,
故答案为:18;
②由①知,四边形ADEB是平行四边形,
∴OA∥DF,
∵以O,A,D,F为顶点的四边形为菱形,
∴OA=AD=DF,
∴∠BAD=60°,
∵∠PAD=90°,
∴∠PAB=30°,
故答案为:30°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】我们在学习“实数”时,画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A”,请根据图形回答下列问题: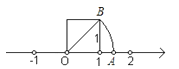
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式,体现了 的数学思想方法.
(将下列符合的选项序号填在横线上)
A、数形结合;B、代入;C、换元;D、归纳.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论.
(2)当点P移动到如图(2)的位置时,∠P与∠A、∠C又有怎样的关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( ).
A.随意掷两个均匀的骰子,朝上面的点数之和为6
B.抛一枚硬币,正面朝上
C.3个人分成两组,一定有2个人分在一组
D.打开电视,正在播放动画片
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动,为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.结合图2和图3回答下列问题:

(1)参加问卷调查的学生人数为 60 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题:
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【定义】配方法是指将一个式子或一个式子的某一部分通过恒等变形华为完全平方式或几个完全平方式的和,这种方法称之为配方法.例如:可将多项式![]() 通过恒等变形化为
通过恒等变形化为![]() 的形式,这个变形过程中应用了配方法.
的形式,这个变形过程中应用了配方法.
【理解】对于多项式![]() ,当
,当![]() = 时,它的最小值为 .
= 时,它的最小值为 .
【应用】若![]() ,求
,求![]() 的值.
的值.
【拓展】![]() 、
、![]() 、
、![]() 是△
是△![]() 的三边,且有
的三边,且有![]() .
.
(1)若![]() 为整数,求
为整数,求![]() 的值.
的值.
(2)若△![]() 是等腰三角形,直接写出这个三角形的周长.
是等腰三角形,直接写出这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中, ![]() 厘米,
厘米, ![]() 厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com