Question

【题目】如图，已知点、、、依次在同一条直线上， ⊥于点， ⊥于点，且＝， ＝.

（1）求证： ∥；

（2）连结、，求证： ＝.

Answer 1

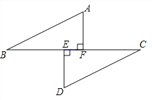
【答案】（1）证明见解析；（2）证明见解析.

【解析】【试题分析】

（1）根据＝，得BF=CE，因为AB=CD,根据两个直角三角形的HL判定定理，得Rt△ABF≌Rt△DCE．根据全等三角形的对应角相等，得∠B=∠C．根据内错角相等，两直线平行，得AB∥DC；

（2）由（1）得：AF=DE,又因为CF=BE, ,根据SAS，得△AFC≌△DEB．根据群等三角形对应边相等，得AC=BD．

【试题解析】

（1）∵AF⊥BC，DE⊥BC，

∴∠DEC=∠AFB=90°．

∵BE=CF，

∴BE+EF=CF+EF．

∴BF=CE．

在Rt△ABF与Rt△DCE中，

∵AB=DC，BF=CE，

∴Rt△ABF≌Rt△DCE．

∴∠B=∠C．

∴AB∥DC．

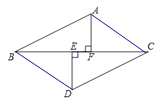
（2）∵Rt△ABF≌Rt△DCE，

∴AF=DE．

∵∠DEB=∠AFC=90°，BE=CF，

∴△AFC≌△DEB．

∴AC=BD．