
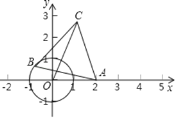
【题目】如图,点O为原点,⊙O的半径为1,点A的坐标为(2,0),动点B在⊙O上,以AB为边作等边△ABC(顺时针),则线段OC的最小值为_____.
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“![]() .非常了解”、“
.非常了解”、“![]() .了解”、“
.了解”、“![]() .基本了解”、“
.基本了解”、“![]() .不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.

(1)这次调查的市民人数为 人,图2中, ![]() ;
;
(2)补全图1中的条形统计图;
(3)在图2中的扇形统计图中,求“![]() .基本了解”所在扇形的圆心角度数;
.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“![]() .不太了解”的市民约有多少万人?
.不太了解”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=40°,∠B=60°,当∠BCD=40°时,证明:CD为△ABC的完美分割线.
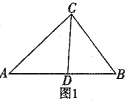
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD是以AC为底边的等腰三角形,求∠ACB的度数.
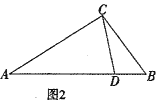
(3)如图2,在△ABC中,AC=2,BC=2,CD是△ABC的完美分割线,△ACD是以CD为底边的等腰三角形,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
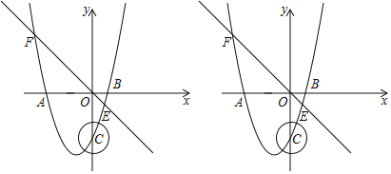
【题目】如图,抛物线y=mx2+nx﹣3(m≠0)与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,直线y=﹣x与该抛物线交于E,F两点.
(1)求点C坐标及抛物线的解析式.
(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.
(3)以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形?若存在,直接写出D点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
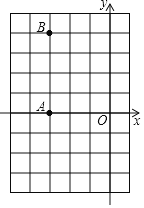
【题目】坐标为整数的点叫格点,如图,已知A(-3,0)、B(-3,4)和原点都是格点,在如图6×9的网格中使用无刻度的直尺按要求作图.
(1)找格点C,连BC,使BC与OA的交点就是OA的中点,画出图形直接写出C点坐标.
(2)按以下方法可以作出∠AOB的平分线.
第一步:找格点D,使OD=OB;
第二步:找格点E,使DE⊥OB交AB于F;
第三步:连OF,则OF是∠AOB的平分线;
请你按步骤完成作图,并写出D、E三点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
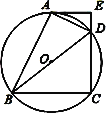
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD交CD的延长线于点E,DA平分∠BDE.
⑴求证:AE是⊙O的切线;
⑵若AE=4cm,CD=6cm,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点M是BC的中点.
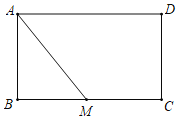
(1)在AM上求作一点E,使△ADE∽△MAB(尺规作图,不写作法);
(2)在(1)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
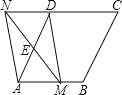
【题目】如图,在菱形ABCD中,AB=4,∠ADN=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N.连接MD、AN,
(1)求证:四边形AMDN是平行四边形;
(2)填空:
①当AM的值为_____时,四边形AMON是矩形;
②当AM的值为______时,四边形AMDN是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若CD=2,AB=8,求半径的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com