
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
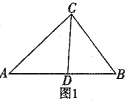
(1)如图1,在△ABC中,∠A=40°,∠B=60°,当∠BCD=40°时,证明:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD是以AC为底边的等腰三角形,求∠ACB的度数.
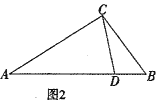
(3)如图2,在△ABC中,AC=2,BC=2,CD是△ABC的完美分割线,△ACD是以CD为底边的等腰三角形,求CD的长.
【答案】(1)证明见解析;(2)∠ACB=96°;(3)CD的长为![]() -1.
-1.
【解析】
(1)根据三角形内角和定理可求出∠ACB=80°,进而可得∠ACD=40°,即可证明AD=CD,由∠BCD=∠A=40°,∠B为公共角可证明三角形BCD∽△BAC,即可得结论;
(2)根据等腰三角形的性质可得∠ACD=∠A=48°,根据相似三角形的性质可得∠BCD=∠A=48°,进而可得∠ACB的度数;
(3)由相似三角形的性质可得∠BCD=∠A,由AC=BC=2可得∠A=∠B,即可证明∠BCD=∠B,可得BD=CD,根据相似三角形的性质列方程求出CD的长即可.
(1)∵∠A=40°,∠B=60°,
∴∠ACB=180°-40°-60°=80°,
∵∠BCD=40°,
∴∠ACD=∠ACB-∠BCD=40°,
∴∠ACD=∠A,
∴AD=CD,即△ACD是等腰三角形,
∵∠BCD=∠A=40°,∠B为公共角,
∴△BCD∽△BAC,
∴CD为△ABC的完美分割线.
(2)∵△ACD是以AC为底边的等腰三角形,
∴AD=CD,
∴∠ACD=∠A=48°,
∵CD是△ABC的完美分割线,
∴△BCD∽△BAC,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(3)∵△ACD是以CD为底边的等腰三角形,
∴AD=AC=2,
∵CD是△ABC的完美分割线,
∴△BCD∽△BAC,
∴∠BCD=∠A,![]() ,
,
∵AC=BC=2,
∴∠A=∠B,
∴∠BCD=∠B,
∴BD=CD,
∴![]() ,即
,即![]() ,
,
解得:CD=![]() -1或CD=-
-1或CD=-![]() -1(舍去),
-1(舍去),
∴CD的长为![]() -1.
-1.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠C=90°.
(1)请你用没有刻度的直尺和圆规,在线段AB上找一点F,使得点F到边AC的距离等于FB.(注:不写作法,保留作图痕迹,对图中涉及到的点的用字母进行标注)
(2)在(1)的情况下,若BC=5,AC=12,则AF= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果![]() (千克),增种果树
(千克),增种果树![]() (棵), 它们之间的函数关系如图所示.
(棵), 它们之间的函数关系如图所示.
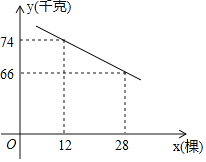
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=4,AD=5,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P在函数y=![]() (x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣
(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣![]() (x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
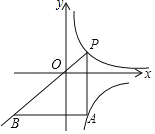
A.逐渐变大B.逐渐变小C.等于定值16D.等于定值24
查看答案和解析>>
科目:初中数学 来源: 题型:
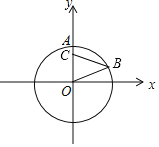
【题目】如图,半径为5的⊙O与y轴相交于A点,B为⊙O在x轴上方的一个动点(不与点A重合),C为y轴上一点且∠OCB=60°,I为△BCO的内心,则△AIO的外接圆的半径的取值(或取值范围)为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
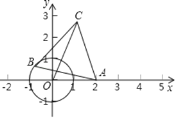
【题目】如图,点O为原点,⊙O的半径为1,点A的坐标为(2,0),动点B在⊙O上,以AB为边作等边△ABC(顺时针),则线段OC的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
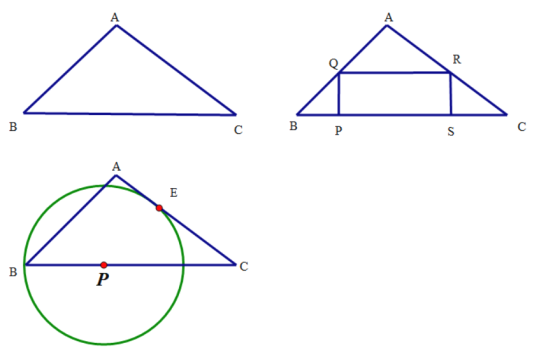
【题目】如图1,在△ABC中,∠ABC=45°,BC=7cm,AB=![]() cm。点P从点B出发沿BC方向向点C运动,当点P到点C时,停止运动
cm。点P从点B出发沿BC方向向点C运动,当点P到点C时,停止运动
(1)如图2,过点P作PQ⊥BC,PQ交AB于点Q,以PQ为一边向右侧作矩形PQRS,若点R恰好在边AC上,且满足QR=2PQ.求BP得值.
(2)以点P为圆心,BP为半径作圆.
①如图3,当⊙P与边AC相切于点E时,求BP的值;
②随着BP的变化,⊙P与△ABC三边的公共点的个数也在变化,请直接写出公共点个数与对应的BP的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com