
【题目】如图,正方形![]() 的边长为9,
的边长为9,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,且
边上的点,且![]() .将
.将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() .
.

(1)求证:![]()
(2)当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)见解析;(2)7.5
【解析】
(1)由旋转可得DE=DM,∠EDM为直角,可得出∠EDF+∠MDF=90°,由∠EDF=45°,得到∠MDF=45°,可得出∠EDF=∠MDF,再由DF=DF,利用SAS可得出三角形DEF与三角形MDF全等,由全等三角形的对应边相等可得出EF=MF;
(2)由第一问的全等得到AE=CM=3,正方形的边长为9,用AB﹣AE求出EB的长,再由BC+CM求出BM的长,设EF=x,可得出BF=BM﹣FM=BM﹣EF=12﹣x,在直角三角形BEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为EF的长.
(1)∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°.
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵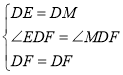 ,
,
∴△DEF≌△DMF(SAS),
∴EF=MF;
(2)设EF=x,则MF=x.
∵AE=CM=3,且BC=9,
∴BM=BC+CM=9+3=12,
∴BF=BM﹣MF=BM﹣EF=12﹣x.
∵EB=AB﹣AE=9﹣3=6,
在Rt△EBF中,由勾股定理得:EB2+BF2=EF2,
即62+(12﹣x)2=x2,
解得:x=7.5,
则EF=7.5.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】知识迁移
当![]() 且
且![]() 时,因为
时,因为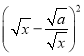 ≥
≥![]() ,所以
,所以![]() ≥
≥![]() ,从而
,从而![]() ≥
≥![]() (当
(当![]() 时取等号).
时取等号).
记函数![]() ,由上述结论可知:当
,由上述结论可知:当![]() 时,该函数有最小值为
时,该函数有最小值为![]()
直接应用
已知函数![]() 与函数
与函数![]() , 则当
, 则当![]() ____时,
____时,![]() 取得最小值为___.
取得最小值为___.
变形应用
已知函数![]() 与函数
与函数![]() ,求
,求![]() 的最小值,并指出取得该最小值时相应的
的最小值,并指出取得该最小值时相应的![]() 的值.
的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共![]() 元;二是燃油费,每千米为
元;二是燃油费,每千米为![]() 元;三是折旧费,它与路程的平方成正比,比例系数为
元;三是折旧费,它与路程的平方成正比,比例系数为![]() .设该汽车一次运输的路程为
.设该汽车一次运输的路程为![]() 千米,求当
千米,求当![]() 为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°
求:(1)求∠ADC的度数;
(2)如果OE⊥AC,垂足为E,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
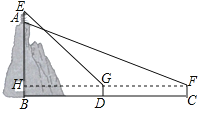
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(![]() 取1.732,结果保留整数)
取1.732,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
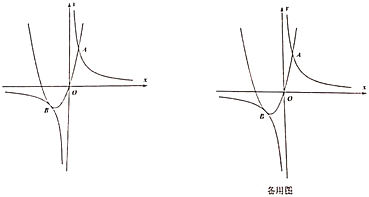
【题目】如图,抛物线![]() (
(![]() )与双曲线
)与双曲线![]() 相交于点
相交于点![]() 、
、![]() ,已知点
,已知点![]() 坐标
坐标![]() ,点
,点![]() 在第三象限内,且
在第三象限内,且![]() 的面积为3(
的面积为3(![]() 为坐标原点).
为坐标原点).
(1)求实数![]() 、
、![]() 、
、![]() 的值;
的值;
(2)在该抛物线的对称轴上是否存在点![]() 使得
使得![]() 为等腰三角形?若存在请求出所有的
为等腰三角形?若存在请求出所有的![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
(3)在坐标系内有一个点![]() ,恰使得
,恰使得![]() ,现要求在
,现要求在![]() 轴上找出点
轴上找出点![]() 使得
使得![]() 的周长最小,请求出
的周长最小,请求出![]() 的坐标和
的坐标和![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
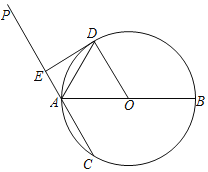
【题目】如图,AB是⊙O的直径,过点A的直线PC交⊙O于A,C两点,AD平分∠PAB,射线AD交⊙O于点D,过点D作DE⊥PA于点E.
(1)求证:ED为⊙O的切线;
(2)若AB=10,ED=2AE,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“![]() .非常了解”、“
.非常了解”、“![]() .了解”、“
.了解”、“![]() .基本了解”、“
.基本了解”、“![]() .不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.

(1)这次调查的市民人数为 人,图2中, ![]() ;
;
(2)补全图1中的条形统计图;
(3)在图2中的扇形统计图中,求“![]() .基本了解”所在扇形的圆心角度数;
.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“![]() .不太了解”的市民约有多少万人?
.不太了解”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
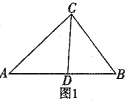
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,∠A=40°,∠B=60°,当∠BCD=40°时,证明:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD是以AC为底边的等腰三角形,求∠ACB的度数.
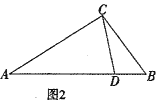
(3)如图2,在△ABC中,AC=2,BC=2,CD是△ABC的完美分割线,△ACD是以CD为底边的等腰三角形,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com