
ЁОЬтФПЁПжЊЪЖЧЈвЦ
ЕБ![]() Чв
Чв![]() ЪБЃЌвђЮЊ
ЪБЃЌвђЮЊ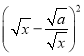 Ён
Ён![]() ,Ыљвд
,Ыљвд![]() Ён
Ён![]() ,ДгЖј
,ДгЖј![]() Ён
Ён![]() (ЕБ
(ЕБ![]() ЪБШЁЕШКХ).
ЪБШЁЕШКХ).
МЧКЏЪ§![]() ,гЩЩЯЪіНсТлПЩжЊЃКЕБ
,гЩЩЯЪіНсТлПЩжЊЃКЕБ![]() ЪБ,ИУКЏЪ§газюаЁжЕЮЊ
ЪБ,ИУКЏЪ§газюаЁжЕЮЊ![]()
жБНггІгУ
вбжЊКЏЪ§![]() гыКЏЪ§
гыКЏЪ§![]() , дђЕБ
, дђЕБ![]() ____ЪБ,
____ЪБ,![]() ШЁЕУзюаЁжЕЮЊ___.
ШЁЕУзюаЁжЕЮЊ___.
БфаЮгІгУ
вбжЊКЏЪ§![]() гыКЏЪ§
гыКЏЪ§![]() ,Чѓ
,Чѓ![]() ЕФзюаЁжЕ,ВЂжИГіШЁЕУИУзюаЁжЕЪБЯргІЕФ
ЕФзюаЁжЕ,ВЂжИГіШЁЕУИУзюаЁжЕЪБЯргІЕФ![]() ЕФжЕ.
ЕФжЕ.
ЪЕМЪгІгУ
вбжЊФГЦћГЕЕФвЛДЮдЫЪфГЩБОАќКЌвдЯТШ§ИіВПЗжЃКвЛЪЧЙЬЖЈЗбгУ,ЙВ![]() дЊЃЛЖўЪЧШМгЭЗб,УПЧЇУзЮЊ
дЊЃЛЖўЪЧШМгЭЗб,УПЧЇУзЮЊ![]() дЊЃЛШ§ЪЧелОЩЗб,ЫќгыТЗГЬЕФЦНЗНГЩе§БШ,БШР§ЯЕЪ§ЮЊ
дЊЃЛШ§ЪЧелОЩЗб,ЫќгыТЗГЬЕФЦНЗНГЩе§БШ,БШР§ЯЕЪ§ЮЊ![]() .ЩшИУЦћГЕвЛДЮдЫЪфЕФТЗГЬЮЊ
.ЩшИУЦћГЕвЛДЮдЫЪфЕФТЗГЬЮЊ![]() ЧЇУз,ЧѓЕБ
ЧЇУз,ЧѓЕБ![]() ЮЊЖрЩйЪБ,ИУЦћГЕЦНОљУПЧЇУзЕФдЫЪфГЩБОзюЕЭЃПзюЕЭЪЧЖрЩйдЊЃП
ЮЊЖрЩйЪБ,ИУЦћГЕЦНОљУПЧЇУзЕФдЫЪфГЩБОзюЕЭЃПзюЕЭЪЧЖрЩйдЊЃП
ЁОД№АИЁПжБНггІгУ 1, 2ЃЛБфаЮгІгУЃК ![]() газюаЁжЕЮЊ
газюаЁжЕЮЊ![]() ,
,![]() ЪБШЁЕУИУзюаЁжЕЃЛЪЕМЪгІгУ2.8
ЪБШЁЕУИУзюаЁжЕЃЛЪЕМЪгІгУ2.8
ЁОНтЮіЁП
жБНгдЫгУЃКПЩвджБНгЬзгУЬтвтЫљИјЕФНсТлЃЌМДПЩЕУГіНсЙћЃЎ
БфаЮдЫгУЃКЯШЕУГі![]() ЕФБэДяЪНЃЌШЛКѓНЋЃЈx+1ЃЉПДзівЛИіећЬхЃЌМЬЖјдйдЫгУЫљИјНсТлМДПЩЃЎ
ЕФБэДяЪНЃЌШЛКѓНЋЃЈx+1ЃЉПДзівЛИіећЬхЃЌМЬЖјдйдЫгУЫљИјНсТлМДПЩЃЎ
ЪЕМЪдЫгУЃКЩшааЪЛxЧЇУзЕФЗбгУЮЊyЃЌдђПЩБэЪОГіЦНОљУПЧЇУзЕФдЫЪфГЩБОЃЌРћгУЫљИјЕФНсТлМДПЩЕУГіД№АИЃЎ
жБНггІгУ 1, 2
БфаЮгІгУ Ёп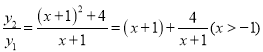
Ёр![]() газюаЁжЕЮЊ
газюаЁжЕЮЊ![]() ,
,
ЕБ![]() ,МД
,МД![]() ЪБШЁЕУИУзюаЁжЕ
ЪБШЁЕУИУзюаЁжЕ
ЪЕМЪгІгУ
НтЃКЩшИУЦћГЕЦНОљУПЧЇУзЕФдЫЪфГЩБОЮЊ![]() дЊ,дђ
дЊ,дђ![]()
![]() ,
,
ЁрЕБ![]() (ЧЇУз)ЪБ, ИУЦћГЕЦНОљУПЧЇУзЕФдЫЪфГЩБО
(ЧЇУз)ЪБ, ИУЦћГЕЦНОљУПЧЇУзЕФдЫЪфГЩБО![]() зюЕЭ
зюЕЭ
зюЕЭГЩБОЮЊ![]() дЊ.
дЊ.


 ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
ЖсЙкбЕСЗЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ
аТЫМЮЌаЁЙкОќ100ЗжзївЕБОЯЕСаД№АИ УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
УћЪІжИЕМвЛОэЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЁїABCжаЃЌAB=ACЃЌADЁЭBCгкЕуDЃЌЗжБ№Й§ЕуAКЭЕуCзїBCЁЂADБпЕФЦНааЯпНЛгкЕуEЃЎ
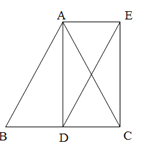
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮADCEЪЧОиаЮЃЛ
ЃЈ2ЃЉСЌНсBEЃЌШє![]() ЃЌAD=
ЃЌAD=![]() ЃЌЧѓBEЕФГЄЃЎ
ЃЌЧѓBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЭјЕъЯњЪлвЛжжЖљЭЏЭцОпЃЌНјМлЮЊУПМў30дЊЃЌЮяМлВПУХЙцЖЈУПМўЖљЭЏЭцОпЕФЯњЪлРћШѓВЛИпгкНјМлЕФ![]() ЃЎдкЯњЪлЙ§ГЬжаЗЂЯжЃЌетжжЖљЭЏЭцОпУПЬьЕФЯњЪлСП
ЃЎдкЯњЪлЙ§ГЬжаЗЂЯжЃЌетжжЖљЭЏЭцОпУПЬьЕФЯњЪлСП![]() ЃЈМў
ЃЈМў![]() гыЯњЪлЕЅМл
гыЯњЪлЕЅМл![]() ЃЈдЊ
ЃЈдЊ![]() ТњзувЛДЮКЏЪ§ЙиЯЕЃЎЕБЯњЪлЕЅМлЮЊ35дЊЪБЃЌУПЬьЕФЯњЪлСПЮЊ350МўЃЛЕБЯњЪлЕЅМлЮЊ40дЊЪБЃЌУПЬьЕФЯњЪлСПЮЊ300МўЃЎ
ТњзувЛДЮКЏЪ§ЙиЯЕЃЎЕБЯњЪлЕЅМлЮЊ35дЊЪБЃЌУПЬьЕФЯњЪлСПЮЊ350МўЃЛЕБЯњЪлЕЅМлЮЊ40дЊЪБЃЌУПЬьЕФЯњЪлСПЮЊ300МўЃЎ
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйЪБЃЌИУЭјЕъЯњЪлетжжЖљЭЏЭцОпУПЬьЛёЕУЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЕФВПЗжЭМЯѓШчЭМЃЌЭМЯѓЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯп
ЕФВПЗжЭМЯѓШчЭМЃЌЭМЯѓЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯп![]() ЃЌЯТСаНсТлЃКЂй
ЃЌЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂмЕБ
ЃЛЂмЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁ ЃЉ
ЕФдіДѓЖјдіДѓЃЎЦфжае§ШЗЕФНсТлгаЃЈЁЁЁЁ ЃЉ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєСНЬѕХзЮяЯпЕФЖЅЕуЯрЭЌЃЌдђГЦЫќУЧЮЊЁАгбКУХзЮяЯпЁБЃЌХзЮяЯпC1ЃКy1=Љ2x2+4x+2гыC2ЃКu2=Љx2+mx+nЮЊЁАгбКУХзЮяЯпЁБЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпC2ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЕуAЪЧХзЮяЯпC2ЩЯдкЕквЛЯѓЯоЕФЖЏЕуЃЌЙ§AзїAQЁЭxжсЃЌQЮЊДЙзуЃЌЧѓAQ+OQЕФзюДѓжЕЃЎ
ЃЈ3ЃЉЩшХзЮяЯпC2ЕФЖЅЕуЮЊCЃЌЕуBЕФзјБъЮЊЃЈЉ1ЃЌ4ЃЉЃЌЮЪдкC2ЕФЖдГЦжсЩЯЪЧЗёДцдкЕуMЃЌЪЙЯпЖЮMBШЦЕуMФцЪБеыа§зЊ90ЁуЕУЕНЯпЖЮMBЁфЃЌЧвЕуBЁфЧЁКУТфдкХзЮяЯпC2ЩЯЃПШєДцдкЧѓГіЕуMЕФзјБъЃЌВЛДцдкЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
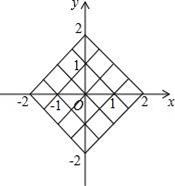
ЁОЬтФПЁП. дквЛИіВЛЭИУїЕФВМДќжазАгаШ§ИіаЁЧђЃЌаЁЧђЩЯЗжБ№БъгаЪ§зжЉ1ЁЂ0ЁЂ2ЃЌЫќУЧГ§СЫЪ§зжВЛЭЌЭтЃЌЦфЫћЖМЭъШЋЯрЭЌЃЎ
ЃЈ1ЃЉЫцЛњЕиДгВМДќжаУўГівЛИіаЁЧђЃЌдђУўГіЕФЧђЮЊБъгаЪ§зж2ЕФаЁЧђЕФИХТЪЮЊ ЃЛ
ЃЈ2ЃЉаЁРіЯШДгВМДќжаЫцЛњУўГівЛИіаЁЧђЃЌМЧЯТЪ§зжзїЮЊЦНУцжБНЧзјБъЯЕФкЕуMЕФКсзјБъЃЎдйНЋДЫЧђЗХЛиЁЂНСдШЃЌШЛКѓгЩаЁЛЊдйДгВМДќжаЫцЛњУўГівЛИіаЁЧђЃЌМЧЯТЪ§зжзїЮЊЦНУцжБНЧзјБъЯЕФкЕуMЕФзнзјБъЃЌЧыгУЪїзДЭМЛђБэИёСаГіЕуMЫљгаПЩФмЕФзјБъЃЌВЂЧѓГіЕуMТфдкШчЭМЫљЪОЕФе§ЗНаЮЭјИёФкЃЈАќРЈБпНчЃЉЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃПЊеЙСЫЁАЛЅжњЁЂЦНЕШЁЂИаЖїЁЂКЭаГЁЂНјШЁЁБжїЬтАрЛсЛюЖЏЃЌЛюЖЏКѓЃЌОЭЛюЖЏЕФ![]() ИіжїЬтНјааСЫГщбљЕїВщЃЈУПЮЛЭЌбЇжЛбЁзюЙизЂЕФвЛИіЃЉЃЌИљОнЕїВщНсЙћЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЎИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ИіжїЬтНјааСЫГщбљЕїВщЃЈУПЮЛЭЌбЇжЛбЁзюЙизЂЕФвЛИіЃЉЃЌИљОнЕїВщНсЙћЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЎИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетДЮЕїВщЕФбЇЩњЙВгаЖрЩйУћЃП
ЃЈ2ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЌВЂдкЩШаЮЭГМЦЭМжаМЦЫуГіЁАНјШЁЁБЫљЖдгІЕФдВаФНЧЕФЖШЪ§ЃЎ
ЃЈ3ЃЉШчЙћвЊдкет![]() ИіжїЬтжаШЮбЁСНИіНјааЕїВщЃЌИљОнЃЈ2ЃЉжаЕїВщНсЙћЃЌгУЪїзДЭМЛђСаБэЗЈЃЌЧѓЧЁКУбЁЕНбЇЩњЙизЂзюЖрЕФСНИіжїЬтЕФИХТЪЃЈНЋЛЅжњЁЂЦНЕШЁЂИаЖїЁЂКЭаГЁЂНјШЁвРДЮМЧЮЊAЁЂBЁЂCЁЂDЁЂEЃЉЃЎ
ИіжїЬтжаШЮбЁСНИіНјааЕїВщЃЌИљОнЃЈ2ЃЉжаЕїВщНсЙћЃЌгУЪїзДЭМЛђСаБэЗЈЃЌЧѓЧЁКУбЁЕНбЇЩњЙизЂзюЖрЕФСНИіжїЬтЕФИХТЪЃЈНЋЛЅжњЁЂЦНЕШЁЂИаЖїЁЂКЭаГЁЂНјШЁвРДЮМЧЮЊAЁЂBЁЂCЁЂDЁЂEЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎЙћХњЗЂЩЬЯњЪлУПЯфНјМлЮЊ40дЊЕФЦЛЙћЃЎОЪаГЁЕїбаЗЂЯжЃКШєУПЯфвд50дЊЕФМлИёЯњЪлЃЌЦНОљУПЬьЯњЪл90ЯфЃЛМлИёУПЬсИп1дЊЃЌдђЦНОљУПЬьЩйЯњЪл3ЯфЃЎЩшУПЯфЕФЯњЪлМлЮЊxдЊЃЈxЃО50ЃЉЃЌЦНОљУПЬьЕФЯњЪлСПЮЊyЯфЃЌИУХњЗЂЩЬЦНОљУПЬьЕФЯњЪлРћШѓwдЊЃЎ
ЃЈ1ЃЉyгыxжЎМфЕФКЏЪ§НтЮіЪНЮЊ__________ЃЛ
ЃЈ2ЃЉЧѓwгыxжЎМфЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЕБxЮЊЖрЩйдЊЪБЃЌПЩвдЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() ЕФБпГЄЮЊ9ЃЌ
ЕФБпГЄЮЊ9ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() БпЩЯЕФЕуЃЌЧв
БпЩЯЕФЕуЃЌЧв![]() .НЋ
.НЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЌЕУЕН
ЃЌЕУЕН![]() .
.

ЃЈ1ЃЉЧѓжЄЃК![]()
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com