练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为估计全市七年级学生的体重情况，从某私立学校随机抽取20人进行调查，在这个问题中，调查的样本________(填“具有”或“不具有”)代表性．

    【答案】不具有

    【解析】

    调查的样本容量不能太少，抽取样本注意事项就是要考虑样本具有广泛性与代表性，应随机抽查．样本具有代表性是指抽取的样本必须是随机的，即各个方面，各个层次的对象都要有所体现．

    为估计全市七年级学生的体重情况，从某私立学校随机抽取20人进行调查，不具有广泛性和代表性．
    故答案为：不具有．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在数轴上有两个点A，B，点A表示﹣3，点B与点A相距5.5个单位长度，则点B表示的数为（ ）
    A.﹣2.5或8.5
    B.2.5或﹣8.5
    C.﹣2.5
    D.﹣8.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若x＋3是4的平方根，则x=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题情境】：
    如图1，AB//CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．
    小明的思路是：过P作PE//AB，通过平行线性质来求∠APC．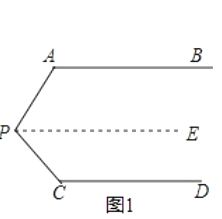

    （1）按小明的思路，求∠APC的度数；
    （2）【问题迁移】：
    如图2，AB//CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；

    （3）【问题应用】：
    在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了“绿色出行”，减少雾霾，家住番禺在广州中心城区上班的王经理，上班出行由自驾车改为乘坐地铁出行，已知王经理家距上班地点21千米，他用地铁方式平均每小时出行的路程，比他用自驾车平均每小时行驶的路程的2倍还多5千米，他从家出发到达上班地点，地铁出行所用时间是自驾车方式所用时间的 ． 求王经理地铁出行方式上班的平均速度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，直L交AB、CD分别于点E、F，点M在线段EF上（点M不与E、F重合），N是直线CD上的一个动点（点N不与F重合）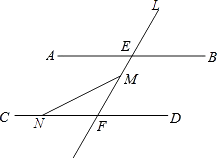

    （1）当点N在射线FC上运动时（F点除外），则∠FMN+∠FNM=∠AEF，说明理由？
    （2）当点N在射线FD上运动时（F点除外），∠FMN+∠FNM与∠AEF有什么关系？画出图形，猜想结论并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图：△ABC中，∠B、∠C的角平分线交于点O，若∠A=60°，则∠BOC=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各组数中，具有相反意义的量是（ ）
    A.身高180cm和身高90cm
    B.向东走5公里和向南走5公里
    C.收入300元和支出300元
    D.使用汽油10公斤和浪费酒精10公斤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果盈利20元记作+20，那么亏本50元记作（ ）
    A.+50元
    B.﹣50元
    C.+20元
    D.﹣20元

    查看答案和解析>>

    同步练习册答案