
【题目】乒乓球是我国的国球,比赛采用单局11分制,是一种世界流行的球类体育项目,比赛分团体、单打、双打等数种在某站公开赛中,某直播平台同时直播4场男单四分之一比赛,四场比赛的球桌号分别为“T1”、“T2”、“T3”、“T4”(假设4场比赛同时开始),小宁和父亲准备一同观看其中的某一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“1、“2”、“3”、“4”的四张卡片(除数字不同外,其余均相同,数字“1”、“2”、“3”、“4”分别对应球桌号(“T1”、“T2”、“T3”、“T4”(背面朝上洗匀,父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛
(1)下列事件中属于必然事件的是
A.抽到的是小宁最终想要看的一场比赛的球桌号
B.抽到的是父亲最终想要看的一场比赛的球桌号
C.小宁和父亲抽到同一个球桌号
D.小宁和父亲抽到的球桌号不一样
(2)用列表法或树状图法求小宁和父亲最终观看“T4”球桌比赛的概率
科目:初中数学 来源: 题型:
【题目】如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )

A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
科目:初中数学 来源: 题型:
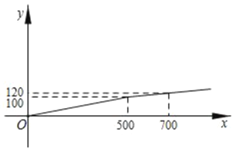
【题目】某校一课外小组准备进行“绿色环保”的宣传活动,需要印刷一批宣传单,学校附近有甲、乙两家印刷社,甲印刷社收费y(元)与印数x(张)的函数关系是:y=0.15x;乙印刷社收费y(元)与印数x(张)的函数关系如图所示:
(1)写出乙印刷社的收费y(元)与印数x(张)之间的函数关系式;
(2)若该小组在甲、乙两印刷社打印了相同数量的宣传单共用去70元,则共打印多少张宣传单?
(3)活动结束后,市民反映良好,兴趣小组决定再加印1500张宣传单,若在甲、乙印刷社中选一家,兴趣小组应选择哪家印刷社比较划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数![]() ,对于函数图象上横坐标之差为1的任意两点
,对于函数图象上横坐标之差为1的任意两点![]() ,
,![]() ,
,![]() 都成立,则称这个函数是限减函数,在所有满足条件的
都成立,则称这个函数是限减函数,在所有满足条件的![]() 中,其最大值称为这个函数的限减系数.例如,函数
中,其最大值称为这个函数的限减系数.例如,函数![]() ,当
,当![]() 取值
取值![]() 和
和![]() 时,函数值分别为
时,函数值分别为![]() ,
,![]() ,故
,故![]() ,因此函数
,因此函数![]() 是限减函数,它的限减系数为
是限减函数,它的限减系数为![]() .
.
(1)写出函数![]() 的限减系数;
的限减系数;
(2)![]() ,已知
,已知![]() (
(![]() )是限减函数,且限减系数
)是限减函数,且限减系数![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)已知函数![]() 的图象上一点
的图象上一点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,将函数
轴,将函数![]() 的图象在点
的图象在点![]() 右侧的部分关于直线
右侧的部分关于直线![]() 翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数
翻折,其余部分保持不变,得到一个新函数的图象,如果这个新函数是限减函数,且限减系数![]() ,直接写出
,直接写出![]() 点横坐标
点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于点A(1,4)和点B(n,
的图象相交于点A(1,4)和点B(n,![]() ).
).
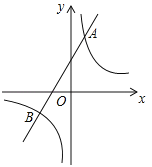
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
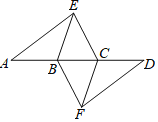
【题目】如图,点A、B、C、D依次在同一条直线上,点E、F分别在直线AD的两侧,已知BE∥CF,∠A=∠D,AE=DF.
(1)求证:四边形BFCE是平行四边形;
(2)填空:若AD=7,AB=2.5,∠EBD=60°,当四边形BFCE是菱形时,菱形BFCE的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com