练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．如图，点I是的内心，点O为△ABC的外心，若∠BOA=140度，则∠BIC的度数为（　　）
    A．100B．120C．125D．135

    分析 利用圆周角定理得出∠C=70°，进而得出利用内心的知识得出∠IBA+∠IAB=55°，即可得出答案．

    解答 解：∵点O为△ABC的外心，∠BOA=140°，
    ∴∠C=70°，
    ∴∠CAB+∠CAB=110°，
    ∵点I为△ABC的内心，
    ∴∠IAB+∠IBA=55°，
    ∴∠AIB=125°．
    故选C．

    点评 此题主要考查了三角形的内心和外心，正确把握三角形内心的性质是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．已知：A-B=7a2-7ab，且A=-4a2+6ab+7，
    （1）求B等于多少？
    （2）若|a+1|+（b-2）2=0，求B的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

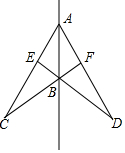    10．如图，线段AC、AD关于直线AB成轴对称，点E、F分别在AC、AD上，且AE=AF．ED、CF相交于点B．图中关于AB成轴对称的三角形共有（　　）
    A．1对B．2对C．3对D．4对

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

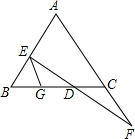    7．如图，已知，EG∥AF，请你从下面三个条件中，再选出两个作为已知条件，另一个作为结论，推出一个正确的命题．并证明这个命题（只写出一种情况）①AB=AC ②DE=DF ③BE=CF 
    已知：EG∥AF，AB=AC，DE=DF．
    求证：BE=CF．
    证明：
    作EG∥AF交BC于G，
    ∴∠EGB=∠ACB，∠GED=∠CFD，
    ∵AB=AC，
    ∴∠B=∠ACB，
    ∴∠B=∠EGB，
    ∴EB=EG，
    在△EGD和△FCD中，
    $\left\{\begin{array}{l}{∠GED=∠CFD}\\{DE=DF}\\{∠GDE=∠CDF}\end{array}\right.$，
    ∴EG=CF，
    ∴BE=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．六边形从一个顶点出发可以引（　　）条对角线．
    A．3B．4C．6D．9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    ①-20+（-14）-（-18）-13
    ②（-81）÷2$\frac{1}{4}$×$\frac{4}{9}$÷（-16）
    ③|-0.75|+（+3$\frac{1}{4}$）-9-（-0.125）+（-$\frac{5}{8}$）-|-0.125|
    ④（$\frac{2}{3}$-$\frac{1}{2}$）×30÷（-$\frac{1}{5}$）
    ⑤（$\frac{1}{6}$-$\frac{2}{3}$+$\frac{3}{7}$）×（-42）
    ⑥1-2+3-4+5-6+…+2015-2016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

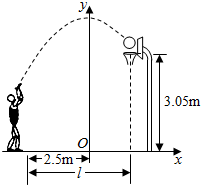    11．小敏在某次投篮中，球的运动线路是抛物线y=-$\frac{1}{5}$x2+3.5的一部分（如图），若命中篮圈中心，则他与篮底的距离l是（　　）
    A．3.5mB．4 mC．4.5 mD．4.6 m

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．小光有60本书，比小英少25%，小英有多少本书？算式是（　　）
    A．60÷25%B．60÷（1-25%）C．60×（1+25%）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

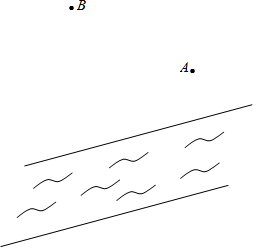    9．如图，A、B两村在一条小河的同一侧，要在河边建一水厂向两村供水．
    （1）若要使自来水厂到两村的距离相等，厂址应选在哪个位置？
    （2）若要使自来水厂到两村的输水管用料最省，厂址应选在哪个位置？请将上述两种情况下的自来水厂厂址标出，并保留作图痕迹．

    查看答案和解析>>

    同步练习册答案