
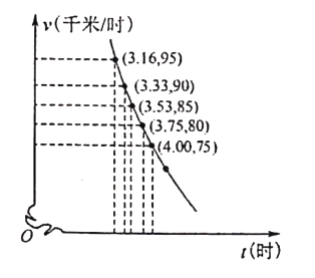
����Ŀ����ˮ����˾������ˮɽ����ũ����Ʒ���������г���������.��������ʻʱ��ΪtСʱ��ƽ���ٶ�Ϊvǧ��/Сʱ��������ʻ�ٶȲ�����100ǧ��/Сʱ��.���ݾ��飬v,t��һ���Ӧֵ���±���
v(ǧ��/Сʱ) | 75 | 80 | 85 | 90 | 95 |
t(Сʱ) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
��1�����ݱ��е����ݣ����ƽ���ٶ�v��ǧ��/Сʱ��������ʻʱ��t(Сʱ)�ĺ�������ʽ��
��2����������7:30����ˮ�������ܷ�������10:00֮ǰ���ﺼ���У���˵�����ɣ�
��3�����������ﺼ���г�����ʻʱ��t����3.5��t��4����ƽ���ٶ�v��ȡֵ��Χ.
���𰸡���1��v= ![]() ����2����������7:30����ˮ����������������10:00֮ǰ���ﺼ���г�����3��ƽ���ٶ�v��ȡֵ��Χ��75��v��
����2����������7:30����ˮ����������������10:00֮ǰ���ﺼ���г�����3��ƽ���ٶ�v��ȡֵ��Χ��75��v�� ![]()
��������
��1�����ݱ��������ݣ���֪v��t�ķ�������������v=![]() �����ô���ϵ�������k���ɣ�
�����ô���ϵ�������k���ɣ�
��2������ʱ��t=2.5������ٶȣ������жϣ�
��3�������Ա�����ȡֵ��Χ���������ֵ��ȡֵ��Χ���ɣ�
��1���⣺��1�����ݱ��е����ݣ��ɻ���v����t�ĺ���ͼ����ͼ��ʾ����
����ͼ����״��ѡ��������ģ�ͽ��г���.��v��t�ĺ�������ʽΪv= ![]() ,
,
�ߵ�v=75ʱ��t=4����k=4��75=300.
��v= ![]() .
.
���㣨3.75,80������3.53,85������3.33,90������3.16��95�����������v= ![]() ��֤��
��֤��
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��v��t�ĺ�������ʽΪv= ![]() .
.
��2���⣺��10-7.5=2.5��
�൱t=2.5ʱ��v= ![]() =120>100.
=120>100.
����������7:30����ˮ����������������10:00֮ǰ���ﺼ���г�.
��3���⣺��ͼ��������������ʵã���3.5��t��4ʱ��75��v�� ![]() .
.
�𰸣�ƽ���ٶ�v��ȡֵ��Χ��75��v�� ![]() .
.


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���E��F��G�ֱ�Ϊ��AB��BC��CD���е㣬����EFG�����Ϊ4�����ı���ABCD�����Ϊ��������
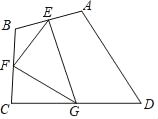
A. 8 B. 12 C. 16 D. 18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼijС������![]() ���������ر�ƫ��
���������ر�ƫ��![]() �ķ����У��ڹ涨��ʱ�佫һ����������
�ķ����У��ڹ涨��ʱ�佫һ����������![]() ���Ļ����ϣ������������߿��ܻ����˳���ʹС����dz�������ı亽�ߣ���
���Ļ����ϣ������������߿��ܻ����˳���ʹС����dz�������ı亽�ߣ���![]() ������������������
������������������![]() ���ﵽ��
���ﵽ��![]() ��������
��������![]() ���ر�ƫ��
���ر�ƫ��![]() �ķ����е���
�ķ����е���![]() ����
����

��1������![]() ��
��![]() ����
����![]() ���˶��ٺ�������ȷ��
���˶��ٺ�������ȷ��![]() �����
�����
��2��Ϊ�˰�ԭ��ʱ�䵽��![]() ���Ļ����ϣ�С�����٣�ÿСʱ����
���Ļ����ϣ�С�����٣�ÿСʱ����![]() �����С��ԭ�����ٶȣ������ȷ��
�����С��ԭ�����ٶȣ������ȷ��![]() ����/ʱ����
����/ʱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���ڵ�A(3,m).
���ڵ�A(3,m).
��1����k��m��ֵ��
��2����֪��P(n��n)(n>0)������P��ƽ����![]() ���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������
���ֱ�ߣ���ֱ��y=x-2�ڵ�M������P��ƽ����y���ֱ�ߣ�������![]() ��ͼ���ڵ�N.
��ͼ���ڵ�N.
�ٵ�n=1ʱ���ж��߶�PM��PN��������ϵ����˵�����ɣ�
����PN��PM����Ϻ�����ͼ��ֱ��д��n��ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ı߳�Ϊ4��EΪAB���е㣬FΪAD��һ�㣬��AF=![]() AD�����жϡ�EFC����״��
AD�����жϡ�EFC����״��
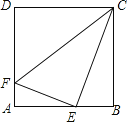
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ���뷴��������![]() ��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������tan��ACO=2��
��m��0����ͼ����A��B���㣬��x�ύ��C�㣬��A������Ϊ��n��6������C������Ϊ����2��0������tan��ACO=2��
��1����÷�����������һ�κ����Ľ���ʽ��
��2�����B�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������4�����ۣ���abc��0����b��a+c����4a+2b+c��0����a+b��m��am+b����m��1��ʵ������������ȷ���۵ĸ���Ϊ��������
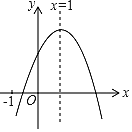
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
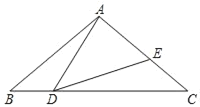
����Ŀ����ͼ������������ABC�У�AB��AC��4����BAC��100�㣬��D�ǵױ�BC�Ķ��㣨��D����B��C�غϣ�������AD������ADE��40�㣬DE��AC���ڵ�E��
��1����DC���ڶ���ʱ����ABD���DCEȫ�ȣ���˵�����ɣ�
��2���ڵ�D���˶������У���ADE����״�����ǵ����������������ԣ������BDA�Ķ������������ԣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ȱߡ�ABC�ı߳�Ϊ8��DΪAC�ϵ�һ�����㣬�ӳ�AB����E��ʹBE=CD������DE��BC�ڵ�P
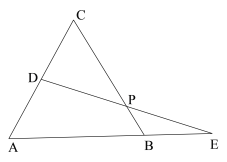
��1����֤��DP=EP��
��2����DΪAC���е㣬��BP�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com