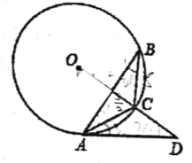
【题目】如图，
内接于
，点
在
的延长线上，
．
（1）求证；
；
（2）若
，求
的长．
【答案】（1）见详解；（2）
【解析】
（1）连接OA，由圆周角定理得∠AOC=60°，则△OAC为等边三角形，则OA⊥AD，得到∠D=30°，即可得到结论成立；
（2）由
，得到∠BAC=30°，则CD=AC=BC=5，然后得到半径OA=OC=5，根据勾股定理，即可求出AD的长度.
解：（1）如图，连接OA，
∵
，
∴
，
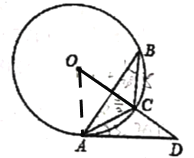
∴△AOC是等边三角形，
∴OA=OC=AC，∠OAC=60°，
∵
，
∴∠OAD=90°，
∴∠D=30°，
∴
，
∴
；
（2）∵，
∴∠BAD+∠D=90°，
∴∠BAD=60°，
∵，
∴∠BAC=30°=∠B，
∴AC=BC=CD=5，
∴OA=OC=AC=5，
∴OD=10，
在Rt△OAD中，由勾股定理，得
.
教材全解字词句篇系列答案科目：初中数学 来源： 题型：
【题目】定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点．
例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P为△ABC的自相似点．
请你运用所学知识，结合上述材料，解决下列问题：
在平面直角坐标系中，点M是曲线C：
上的任意一点，点N是x轴正半轴上的任意一点．
（1） 如图2，点P是OM上一点，∠ONP=∠M, 试说明点P是△MON的自相似点； 当点M的坐标是
，点N的坐标是
时，求点P 的坐标；
（2） 如图3，当点M的坐标是
，点N的坐标是
时，求△MON的自相似点的坐标；
（3） 是否存在点M和点N,使△MON无自相似点,？若存在，请直接写出这两点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
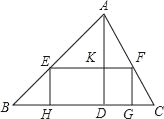
【题目】在锐角△ABC中，边BC长为18，高AD长为12
（1）如图，矩形EFCH的边GH在BC边上，其余两个顶点E、F分别在AB、AC边上，EF交AD于点K，求
的值；
（2）设EH＝x，矩形EFGH的面积为S，求S与x的函数关系式，并求S的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在面积为60的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB=10，BC=12，则CE+CF的值为（ ）
A. 22-11
B. 
C. 或
D. 
或
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=ax2﹣8ax+12a（a＜0）与x轴交于A、B两点(点A在点B的左边)，抛物线上另有一点C在第一象限，且使△OCA∽△OBC，
（1）求OC的长及
的值；
（2）设直线BC与y轴交于P点，当点C恰好在OP的垂直平分线上时，求直线BP和抛物线的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某兴趣小组为了了解本校学生参加课外体育锻炼情况，随机抽取本校40名学生进行问卷调查，统计整理并绘制了如下两幅尚不完整的统计图：
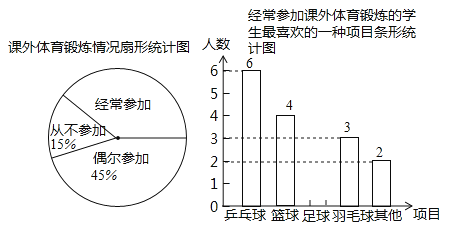
根据以上信息解答下列问题：
（1）课外体育锻炼情况统计图中，“经常参加”所对应的圆心角的度数为 ；“经常参加课外体育锻炼的学生最喜欢的一种项目”中，喜欢足球的人数有 人，补全条形统计图．
（2）该校共有1200名学生，请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人？
（3）若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组，请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
