
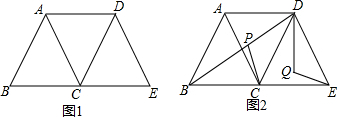
分析 (1)直接由等边三角形的性质即可得出即可;
(2)①先判断PD=DQ,∠PDQ=60°,进而判断出△DPC≌△DQE即可得出结论;
②先判断出△DPQ是等边三角形,进而得出DP=DQ,再判断出点A、P、Q、E在同一直线上(AE)时,AP+CP+DP的值最小.
解答 解:(1)答案不唯一,合理即可,
AD∥BE,四边形ABCD、ACED是菱形;
四边形ABED是等腰梯形;四边形ABED是轴对称图形;
理由:∵△ABC、△ACD和△CDE是等边三角形,
∴∠ACB=∠CAD=60°,
∴AD∥BE.
∵△ABC、△ACD和△CDE是等边三角形,
∴AB=BC=CD=AD=DE=CE,
∴四边形ABCD、ACED是菱形,四边形ABED是等腰梯形;
(2)①CP=QE;理由:
∵△AEC是等边三角形,
∴CD=DE,∠CDE=60°,
∵DP绕点D逆时针旋转60°到DQ,
∴PD=DQ,∠PDQ=60°,
∴∠PDQ=∠QDE,
∴△DPC≌△DQE
∴CP=QE.
②如图1,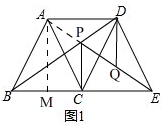 连接AP,由①可知CP=QE,
连接AP,由①可知CP=QE,
∵DP绕点D逆时针旋转60°到DQ,
∴△DPQ是等边三角形,
∴DP=DQ,
要使AP+CP+DP的值最小,
∴AP+QE+QP的值最小,
即点A、P、Q、E在同一直线上(AE),构建两点之间,线段最短,
过点A作AM⊥BE于点M,可得BM=1,EM=3,AM=$\sqrt{3}$,
所以AE=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,
故在BD上存在点P,故AP+CP+DP的值最小,最小值是$2\sqrt{3}$.
点评 此题是几何变换综合题,主要考查了等边三角形的性质和判定,菱形的判定,等腰梯形的性质,全等三角形的判定和性质,解(2)①的关键是判断出∠PDQ=∠QDE,解(2)②的关键是判断出点A、P、Q、E在同一直线上(AE)时,AP+CP+DP的值最小,是一道基础题目.


科目:初中数学 来源: 题型:选择题
 中国讲究五谷丰登,六畜兴旺.如图是一个正方体展开图,图中的六个正方形内分别标有六畜:“猪”、“牛”、“羊”、“马”、“鸡”、“狗”.将其围成一个正方体后,则与“牛”相对的是( )
中国讲究五谷丰登,六畜兴旺.如图是一个正方体展开图,图中的六个正方形内分别标有六畜:“猪”、“牛”、“羊”、“马”、“鸡”、“狗”.将其围成一个正方体后,则与“牛”相对的是( )| A. | 羊 | B. | 马 | C. | 鸡 | D. | 狗 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
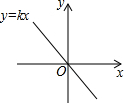 已知函数y=kx的图象如图所示,则对一元二次方程x2+x+k-1=0根的情况,说法正确的是( )
已知函数y=kx的图象如图所示,则对一元二次方程x2+x+k-1=0根的情况,说法正确的是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780-1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845-1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780-1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845-1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )| A. | 5 | B. | 4 | C. | $3+\sqrt{2}$ | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
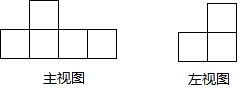 如图是由大小相同的小正方体搭成的几何体的主视图和左视图,搭成这样的几何体最多需要a个这样的小正方体,则a=( )
如图是由大小相同的小正方体搭成的几何体的主视图和左视图,搭成这样的几何体最多需要a个这样的小正方体,则a=( )| A. | 16 | B. | 12 | C. | 9 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
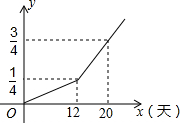 甲、乙两个工程队共同完成一项工程,先由甲单独做,然后乙队加入,两个工程队合作完成余下工程,工程的进度y与甲工作的时间x(天)的函数关系如图所示,则乙队单独完成此项工程需24天.
甲、乙两个工程队共同完成一项工程,先由甲单独做,然后乙队加入,两个工程队合作完成余下工程,工程的进度y与甲工作的时间x(天)的函数关系如图所示,则乙队单独完成此项工程需24天.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com