
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是 .
(k<0)上运动,则k的值是 . 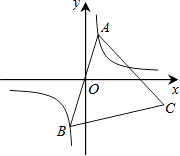
【答案】﹣6
【解析】解:∵双曲线y= ![]() 关于原点对称, ∴点A与点B关于原点对称.
关于原点对称, ∴点A与点B关于原点对称.
∴OA=OB.
连接OC,如图所示.
∵△ABC是等边三角形,OA=OB,
∴OC⊥AB.∠BAC=60°.
∴tan∠OAC= ![]() =
= ![]() .
.
∴OC= ![]() OA.
OA.
过点A作AE⊥y轴,垂足为E,
过点C作CF⊥y轴,垂足为F,
∵AE⊥OE,CF⊥OF,OC⊥OA,
∴∠AEO=∠OFC,∠AOE=90°﹣∠FOC=∠OCF.
∴△AEO∽△OFC.
∴ ![]() =
= ![]() =
= ![]() .
.
∵OC= ![]() OA,
OA,
∴OF= ![]() AE,FC=
AE,FC= ![]() EO.
EO.
设点A坐标为(a,b),
∵点A在第一象限,
∴AE=a,OE=b.
∴OF= ![]() AE=
AE= ![]() a,FC=
a,FC= ![]() EO=
EO= ![]() b.
b.
∵点A在双曲线y= ![]() 上,
上,
∴ab=2.
∴FCOF= ![]() b
b ![]() a=3ab=6
a=3ab=6
设点C坐标为(x,y),
∵点C在第四象限,
∴FC=x,OF=﹣y.
∴FCOF=x(﹣y)=﹣xy
=6.
∴xy=﹣6.
∵点C在双曲线y= ![]() 上,
上,
∴k=xy=﹣6.
故答案为:﹣6.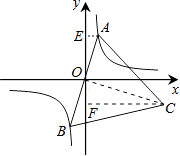
连接OC,易证AO⊥OC,OC= ![]() OA.由∠AOC=90°想到构造K型相似,过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,可证△AEO∽△OFC.从而得到OF=
OA.由∠AOC=90°想到构造K型相似,过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,可证△AEO∽△OFC.从而得到OF= ![]() AE,FC=
AE,FC= ![]() EO..设点A坐标为(a,b)则ab=2,可得FCOF=6.设点C坐标为(x,y),从而有FCOF=﹣xy=﹣6,即k=xy=﹣6.
EO..设点A坐标为(a,b)则ab=2,可得FCOF=6.设点C坐标为(x,y),从而有FCOF=﹣xy=﹣6,即k=xy=﹣6.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,添加下列条件,还不能使△ABC≌△CDA成立的是( )

A. AD=BC B. ∠BAC=∠ACD C. AB∥DC D. AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)试验探索:
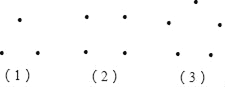
如果过每两点可以画一条直线,那么请下面三组图中分别画线,并回答问题:
第(1)组最多可以画______条直线;
第(2)组最多可以画______条直线;
第(3)组最多可以画______条直线.
(2)归纳结论:
如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画出直线______条.(作用含n的代数式表示)
(3)解决问题:
某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物.
查看答案和解析>>
科目:初中数学 来源: 题型:
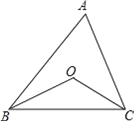
【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点在坐标轴上,点A的坐标为(﹣3,0),假设有甲,乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按顺时针方向匀速运动,物体乙按逆时针方向匀速运动,若物体甲12秒钟可环绕一周回到点A,物体乙24秒钟可环绕一周回到点A,则两个物体运动后的第2017次相遇地点的坐标是 . 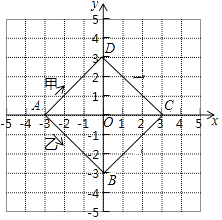
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图长方形MNPQ是菜市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
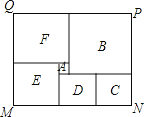
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOD=150°,OB、OC、OM、ON 是∠AOD 内的射线,若∠BOC=20°,∠AOB=10°,OM 平分∠AOC,ON 平分∠BOD,当∠BOC 在∠AOD 内绕着点 O以 3°/秒的速度逆时针旋转 t 秒时,当∠AOM:∠DON=3:4 时,则 t=____________.
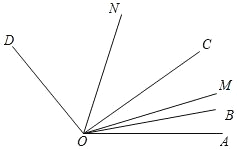
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com