
【题目】如图,在平行四边形ABCD中,点E为边DC上一点,且DE∶EC=3∶1,连接AE并延长,与BC的延长线交于点G,AE与BD交于点F,则△GEC的面积与△DEF的面积之比为( )
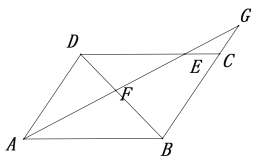
A.1∶3B.3∶7C.4∶21D.7∶27
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】某中学举行“中国梦,我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
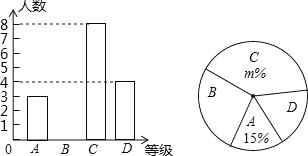
(1)参加比赛的学生共有 名,在扇形统计图中,表示“D等级”的扇形的圆心角为 度,图中m的值为 ;
(2)补全条形统计图;
(3)组委会决定分别从本次比赛中获利A、B两个等级的学生中,各选出1名学生培训后搭档去参加市中学生演讲比赛,已知甲的等级为A,乙的等级为B,求同时选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______.
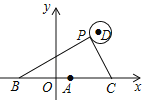
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在使用笔记本电脑时,为了散热,他将电脑放在散热架CAD上,忽略散热架和电脑的厚度,侧面示意图如图1所示,已知电脑显示屏OB与底板OA的夹角为135°,OB=OA=25cm,OE⊥AD于点E,OE=12.5cm.

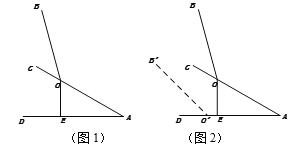
(1)求∠OAE的度数;
(2)若保持显示屏OB与底板OA的135°夹角不变,将电脑平放在桌面上如图2中的![]() 所示,则显示屏顶部
所示,则显示屏顶部![]() 比原来顶部B大约下降了多少?(参考数据:结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,
比原来顶部B大约下降了多少?(参考数据:结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.已知两车相遇时快车比慢车多行驶60千米.若快车从甲地到达乙地所需时间为t时,则此时慢车与甲地相距_____千米.
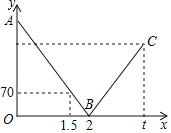
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )

A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,﹣2).
,且点B的坐标为(n,﹣2).
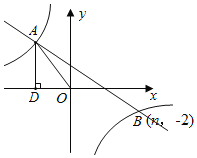
(1)求一次函数与反比例函数的解析式;
(2)请直接写出满足kx+b>![]() 的x的取值范围;
的x的取值范围;
(3)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com