
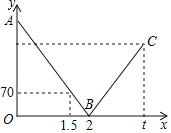
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.已知两车相遇时快车比慢车多行驶60千米.若快车从甲地到达乙地所需时间为t时,则此时慢车与甲地相距_____千米.
【答案】![]()
【解析】
求出相遇前y与x的关系式,确定出甲乙两地的距离,进而求出两车的速度,即可求解.
设AB所在直线的解析式为:y=kx+b,
把(1.5,70)与(2,0)代入得:
![]() ,
,
解得:![]() ,
,
∴AB所在直线的解析式为:y=-140x+280,
令x=0,得到y=280,即甲乙两地相距280千米,
设两车相遇时,乙行驶了x千米,则甲行驶了(x+60)千米,
根据题意得:x+x+60=280,
解得:x=110,即两车相遇时,乙行驶了110千米,甲行驶了170千米,
∴甲车的速度为85千米/时,乙车速度为55千米/时,
根据题意得:280﹣55×(280÷85)=![]() (千米).
(千米).
则快车到达乙地时,慢车与甲地相距![]() 千米.
千米.
故答案为:![]()


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚筒轮⊙A,⊙A与水平地面相切于点D,在拉杆伸长到最大的情况下,当点B距离水平地面34cm时,点C到水平地面的距离CE为55cm.设AF∥ MN.
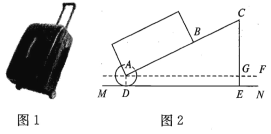
(1)求⊙A的半径.
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果精确到1cm,参考数据:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
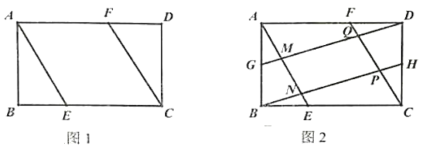
【题目】如图1,在矩形ABCD中AB=4, BC=8,点E、F是BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形.
(2)如果四边形AECF是菱形,求这个菱形的边长.
(3)如图2,在(2)的条件下,取AB、CD的中点G、H,连接DG、BH, DG分别交AE、CF于点M、Q, BH分别交AE、CF于点N、P,求点P到BC的距离并直接写出四边形MNPQ的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为边DC上一点,且DE∶EC=3∶1,连接AE并延长,与BC的延长线交于点G,AE与BD交于点F,则△GEC的面积与△DEF的面积之比为( )
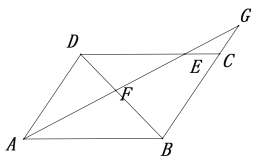
A.1∶3B.3∶7C.4∶21D.7∶27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在一节数学活动课上,老师带领同学们借助几何画板对以下题目进行了研究.如图1,
MN是过点A的直线,点C为直线MN外一点,连接AC,作∠ACD=60°,使AC=DC,在MN上取一点B,使∠DBN=60°.
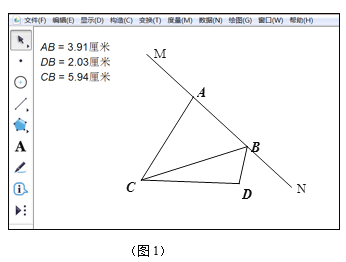
观察发现
(1)根据图1中的数据,猜想线段AB、DB、CB之间满足的数量关系是 ;
(2)希望小组认真思考后提出一种证明方法:将CB所在的直线以点C为旋转中心,逆时针旋转60°,与直线MN交于点E,即可证明(1)中的结论. 请你在图1中作出线段CE,并根据此方法写出证明过程;
实践探究
(3)奋进小组在继续探究的过程中,将点C绕点A逆时针旋转,他们发现当旋转到图2和图3的位置时,∠DBN=120°,线段AB、BD、CB的大小发生了变化,但是仍然满足一定的数量关系,请你直接写出这两种关系:
在图2中,线段AB、DB、CB之间满足的数量关系是 ;
在图3中,线段AB、DB、CB之间满足的数量关系是 ;
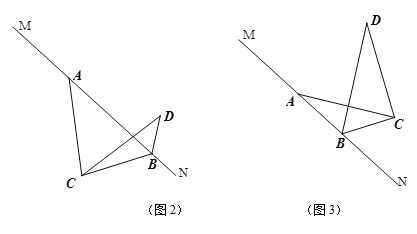
提出问题
(4)智慧小组提出一个问题:若图3中BC⊥CD于点C时,BC=2,则AC为多长?请你解答此问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点E是AD边上的点,连接BE.
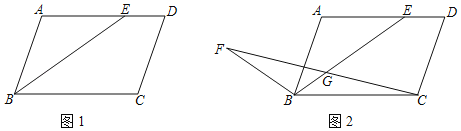
(1)如图1,若BE平分∠ABC,BC=8,ED=3,求平行四边形ABCD的周长;
(2)如图2,点F是平行四边形外一点,FB=CD.连接BF、CF,CF与BE相交于点G,若∠FBE+∠ABC=180°,点G是CF的中点,求证:2BG+ED=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用铁片制作的圆锥形容器盖如图所示.
(1)我们知道:把平面内线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆.类比圆的定义,给圆锥下定义 ;
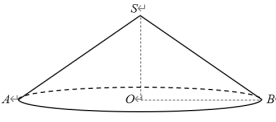
(2)已知OB=2 cm,SB=3 cm,
①计算容器盖铁皮的面积;
②在一张矩形铁片上剪下一个扇形,用它围成该圆锥形容器盖.以下是可供选用的矩形铁片的长和宽,其中可以选择且面积最小的矩形铁片是 .
A.6 cm×4 cm B.6 cm×4.5 cm C.7 cm×4 cm D.7 cm×4.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因抖音等新媒体的传播,西安已成为最著名的网红旅游城市之一,2018年“十一”黄金周期间,接待游客已达![]() 万人次,古城西安美食无数,一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗
万人次,古城西安美食无数,一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗![]() 元,借鉴以往经验;若每碗小面卖
元,借鉴以往经验;若每碗小面卖![]() 元,平均每天能够销售
元,平均每天能够销售![]() 碗,若降价销售,毎降低
碗,若降价销售,毎降低![]() 元,则平均每天能够多销售
元,则平均每天能够多销售![]() 碗.为了维护城市形象,店家规定每碗小面的售价不得超过
碗.为了维护城市形象,店家规定每碗小面的售价不得超过![]() 元,则当每碗小面的售价定为多少元时,店家才能实现每天盈利
元,则当每碗小面的售价定为多少元时,店家才能实现每天盈利![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
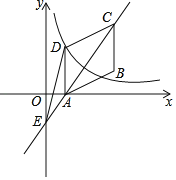
(1)写出D点坐标;
(2)求双曲线的解析式;
(3)作直线AC交y轴于点E,连结DE,求△CDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com