
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚筒轮⊙A,⊙A与水平地面相切于点D,在拉杆伸长到最大的情况下,当点B距离水平地面34cm时,点C到水平地面的距离CE为55cm.设AF∥ MN.
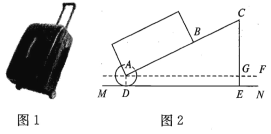
(1)求⊙A的半径.
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果精确到1cm,参考数据:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】若抛物线![]() (
(![]() 是常数,
是常数,![]() )与直线
)与直线![]() 都经过
都经过![]() 轴上的一点
轴上的一点![]() ,且抛物线
,且抛物线![]() 的顶点
的顶点![]() 在直线
在直线![]() 上,则称此直线
上,则称此直线![]() 与该抛物线
与该抛物线![]() 具有“一带一路”关系.此时,直线
具有“一带一路”关系.此时,直线![]() 叫做抛物线
叫做抛物线![]() 的“带线”,抛物线
的“带线”,抛物线![]() 叫做直线
叫做直线![]() 的“路线”.
的“路线”.
(1)若直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,求
具有“一带一路”关系,求![]() 的值;
的值;
(2)若某“路线”![]() 的顶点在反比例函数
的顶点在反比例函数![]() 的图象上,它的“带线”
的图象上,它的“带线”![]() 的解析式为
的解析式为![]() ,求此“路线”
,求此“路线”![]() 的解析式;
的解析式;
(3)当常数![]() 满足
满足![]() 时,请直接写出抛物线
时,请直接写出抛物线![]() :
:![]() 的“带线”
的“带线”![]() 与
与![]() 轴,
轴,![]() 轴所围成的三角形面积S的取值范围.
轴所围成的三角形面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
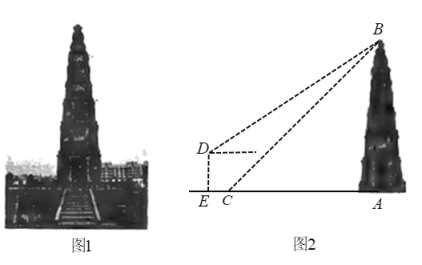
【题目】如图1,在唐河县文峰广场,耸立着一座古老建筑-文峰塔,传说唐河县城是一个船地, 唐中是船头,文峰塔是船的桅杆,无论唐河水怎么涨,唐河县城这艘船也水涨船高.学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量文峰塔的高度.如图2,刘明在点![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() 王华在高台上的点
王华在高台上的点![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() ,若高台
,若高台![]() 高为
高为![]() 米,点
米,点![]() 到点
到点![]() 的水平距离EC为
的水平距离EC为![]() 米,且
米,且![]() 三点共线,求该塔
三点共线,求该塔![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,结果保留整数)
,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
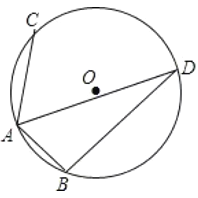
【题目】如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为 _____________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
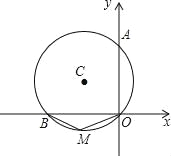
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大变化,其体温(![]() )与时间(小时)之间的关系如图1所示.
)与时间(小时)之间的关系如图1所示.

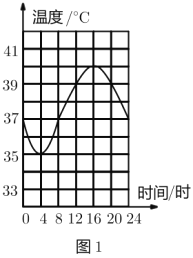
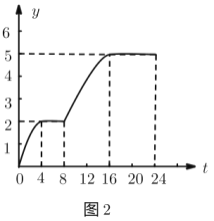
小清同学根据图1绘制了图2,则图2中的变量有可能表示的是( ).
A.骆驼在![]() 时刻的体温与0时体温的绝对差(即差的绝对值)
时刻的体温与0时体温的绝对差(即差的绝对值)
B.骆驼从0时到![]() 时刻之间的最高体温与当日最低体温的差
时刻之间的最高体温与当日最低体温的差
C.骆驼在![]() 时刻的体温与当日平均体温的绝对差
时刻的体温与当日平均体温的绝对差
D.骆驼从0时到![]() 时刻之间的体温最大值与最小值的差
时刻之间的体温最大值与最小值的差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 到封闭图形
到封闭图形![]() 的“极化距离”
的“极化距离”![]()
![]() 定义如下:任取图形
定义如下:任取图形![]() 上一点
上一点![]() ,记
,记![]() 长度的最大值为
长度的最大值为![]() ,最小值为
,最小值为![]() (若
(若![]() 与
与![]() 重合,则
重合,则![]() ),则“极化距离”
),则“极化距离”![]() .
.

(1)如图1,正方形![]() 以原点
以原点![]() 为中心,点
为中心,点![]() 的坐标为
的坐标为![]() ,
,
①点![]() 到线段
到线段![]() 的“极化距离”
的“极化距离”![]() _______;
_______;
点![]() 到线段
到线段![]() 的“极化距离”
的“极化距离”![]() _________;
_________;
②记正方形![]() 为图形
为图形![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)如图2,图形![]() 为圆心
为圆心![]() 在
在![]() 轴上,半径为
轴上,半径为![]() 的圆,直线
的圆,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 上的任一点
上的任一点![]() 都满足
都满足![]() ,直接写出圆心
,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() ,直线
,直线![]() .
.
(1)当![]() 时,求抛物线与
时,求抛物线与![]() 轴交点的坐标;
轴交点的坐标;
(2)直线是否可能经过抛物线的顶点,如果可能,请求出![]() 的值,如果不可能,请说明理由;
的值,如果不可能,请说明理由;
(3)记![]() ,当
,当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
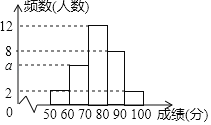
【题目】为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,己知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为 ;
(2)若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为 度;
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有 人:
(4)在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com