
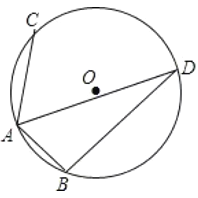
【题目】如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为 _____________ .
【答案】4![]()
【解析】
连结BC、OB、OC,延长DO交BC与H,利用角平分线定义得∠BAD=∠CAD=![]() ∠BAC=60°,则根据圆周角定理得到∠DBC=∠BCD=60°,于是可判断△BCD为等边三角形,所以BD=BC,∠BDC=60°;再利用∠ABD=∠CAD得到弧DC=弧DB,根据垂径定理的推论得到DH⊥BC,BH=CH,接着根据圆周角定理计算出∠BOH=60°,然后在Rt△BOH中根据含30度的直角三角形三边的关系可计算出BH=2
∠BAC=60°,则根据圆周角定理得到∠DBC=∠BCD=60°,于是可判断△BCD为等边三角形,所以BD=BC,∠BDC=60°;再利用∠ABD=∠CAD得到弧DC=弧DB,根据垂径定理的推论得到DH⊥BC,BH=CH,接着根据圆周角定理计算出∠BOH=60°,然后在Rt△BOH中根据含30度的直角三角形三边的关系可计算出BH=2![]() ,则BC=2BH=4
,则BC=2BH=4![]() ,即BD=
,即BD=![]() .
.
解:连结BC、OB、OC,延长DO交BC与H,如图,
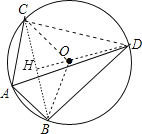
∵AD平分∠BAC,
∴∠BAD=∠CAD=![]() ∠BAC=60°,
∠BAC=60°,
∴∠DBC=∠BCD=60°,
∴△BCD为等边三角形,
∴BD=BC,∠BDC=60°,
∵∠ABD=∠CAD,
∴弧DC=弧DB,
∴DH⊥BC,
∴BH=CH,∠BOH=![]() ∠BOC,
∠BOC,
而∠BOC=2∠BDC=120°,
∴∠BOH=60°,
在Rt△BOH中,∵∠OBH=30°,
∴OH=![]() OB=2,
OB=2,
∴BH=![]() OH=
OH=![]() ,
,
∴BC=2BH=![]() ,
,
∴BD=![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,已知
轴上,已知![]() ,抛物线
,抛物线![]() (其中
(其中![]() )经过
)经过![]() 三点,双曲线
三点,双曲线![]() (其中
(其中![]() )经过点
)经过点![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 且
且![]()
(1)求出![]() 的值;当
的值;当![]() 为直角三角形时,请求出
为直角三角形时,请求出![]() 的表达式;
的表达式;
(2)当![]() 为正三角形时,直线
为正三角形时,直线![]() 平分
平分![]() ,求
,求![]() 时
时![]() 的取值范围;
的取值范围;
(3)抛物线![]() (其中
(其中![]() )有一时刻恰好经过
)有一时刻恰好经过![]() 点,且此时抛物线与双曲线
点,且此时抛物线与双曲线![]() (其中
(其中![]() )有且只有一个公共点
)有且只有一个公共点![]() (其中
(其中![]() ),我们不妨把此时刻的
),我们不妨把此时刻的![]() 记作
记作![]() ,请直接写出抛物线
,请直接写出抛物线![]() (其中
(其中![]() )与双曲线
)与双曲线![]() (其中
(其中![]() )有一个公共点时
)有一个公共点时![]() 的取值范围.(
的取值范围.(![]() 是已知数)
是已知数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某个函数,若自变量取实数![]() ,其函数值恰好也等于
,其函数值恰好也等于![]() 时,则称
时,则称![]() 为这个函数的“等量值”.在函数存在“等量值”时,该函数的最大“等量值”与最小“等量值”的差
为这个函数的“等量值”.在函数存在“等量值”时,该函数的最大“等量值”与最小“等量值”的差![]() 称为这个函数的“等量距离”,特别地,当函数只有一个“等量值”时,规定其“等最距离”
称为这个函数的“等量距离”,特别地,当函数只有一个“等量值”时,规定其“等最距离”![]() 为0.
为0.
(1)请分别判断函数![]() ,
,![]() ,
,![]() 有没有“等量值”?如果有,直接写出其“等量距离”;
有没有“等量值”?如果有,直接写出其“等量距离”;
(2)已知函数![]() .
.
①若其“等量距离”为0,求![]() 的值;
的值;
②若![]() ,求其“等量距离”
,求其“等量距离”![]() 的取值范围;
的取值范围;
③若“等量距离”![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ACB=90°,∠A=30°,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=_____时,平行四边形CDEB为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2![]() ,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.

(1)求经过点O,C,A三点的抛物线的解析式.
(2)若点M是抛物线上一点,且位于线段OC的上方,连接MO、MC,问:点M位于何处时三角形MOC的面积最大?并求出三角形MOC的最大面积.
(3)抛物线上是否存在一点P,使∠OAP=∠BOC?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
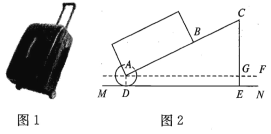
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚筒轮⊙A,⊙A与水平地面相切于点D,在拉杆伸长到最大的情况下,当点B距离水平地面34cm时,点C到水平地面的距离CE为55cm.设AF∥ MN.
(1)求⊙A的半径.
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果精确到1cm,参考数据:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC![]() ,求EC的长.
,求EC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com