
ЁОЬтФПЁПвбжЊЃЎдкRtЁїOABжаЃЌЁЯOAB=90ЁуЃЌЁЯBOA=30ЁуЃЌOA=2![]() ЃЌШєвдOЮЊзјБъдЕуЃЌOAЫљдкжБЯпЮЊxжсЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЕуBдкЕквЛЯѓЯоФкЃЌНЋRtЁїOABбиOBелЕўКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуCДІЃЎ
ЃЌШєвдOЮЊзјБъдЕуЃЌOAЫљдкжБЯпЮЊxжсЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЕуBдкЕквЛЯѓЯоФкЃЌНЋRtЁїOABбиOBелЕўКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуCДІЃЎ

ЃЈ1ЃЉЧѓОЙ§ЕуOЃЌCЃЌAШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШєЕуMЪЧХзЮяЯпЩЯвЛЕуЃЌЧвЮЛгкЯпЖЮOCЕФЩЯЗНЃЌСЌНгMOЁЂMCЃЌЮЪЃКЕуMЮЛгкКЮДІЪБШ§НЧаЮMOCЕФУцЛ§зюДѓЃПВЂЧѓГіШ§НЧаЮMOCЕФзюДѓУцЛ§ЃЎ
ЃЈ3ЃЉХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁЯOAP=ЁЯBOCЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2+2![]() xЃЛЃЈ2ЃЉ
xЃЛЃЈ2ЃЉ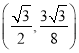 ,
,![]() ЃЛЃЈ3ЃЉДцдкЃЌP(
ЃЛЃЈ3ЃЉДцдкЃЌP(![]() ЃЌ
ЃЌ![]() )Лђ(Љ
)Лђ(Љ![]() ЃЌЉ
ЃЌЉ![]() )
)
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнелЕўЕФаджЪПЩЕУOC=OAЃЌЁЯBOC=ЁЯBAO=30ЁуЃЌЙ§ЕуCзїCDЁЭOAгкDЃЌЧѓГіODЁЂCDЃЌШЛКѓаДГіЕуCЕФзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪННтД№ЃЛ
ЃЈ2ЃЉЧѓГіжБЯпOCЕФНтЮіЪНЃЌИљОнЕуMЕНOCЕФзюДѓОрРыЪБЃЌУцЛ§зюДѓЃЛЦНаагкOCЕФжБЯпгыХзЮяЯпжЛгавЛИіНЛЕуЃЌРћгУИљЕФХаБ№ЪНЧѓГіmЕФжЕЃЌРћгУШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЧѓГіжБЯпAPгыyжсЕФНЛЕузјБъЃЌШЛКѓЧѓГіжБЯпAPЕФНтЮіЪНЃЌгыХзЮяЯпНтЮіЪНСЊСЂЧѓНтМДПЩЕУЕНЕуPЕФзјБъЃЎ
НтЃКЃЈ1ЃЉЁпRtЁїOABбиOBелЕўКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуCДІЃЌ
ЁрOC=OA=2![]() ЃЌЁЯBOC=ЁЯBAO=30ЁуЃЌ
ЃЌЁЯBOC=ЁЯBAO=30ЁуЃЌ
ЁрЁЯAOC=30Ёу+30Ёу=60ЁуЃЌ
Й§ЕуCзїCDЁЭOAгкDЃЌ
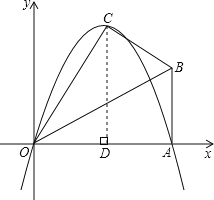
дђOD=![]() ЁС2
ЁС2![]() =
=![]() ЃЌ
ЃЌ
CD=2![]() ЁС
ЁС![]() =3ЃЌ
=3ЃЌ
ЫљвдЃЌЖЅЕуCЕФзјБъЮЊЃЈ![]() ЃЌ3ЃЉЃЌ
ЃЌ3ЃЉЃЌ
ЩшЙ§ЕуOЃЌCЃЌAХзЮяЯпЕФНтЮіЪНЮЊЮЊy=ax2+bxЃЌ
дђ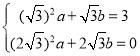 ЃЌ
ЃЌ
НтЕУЃК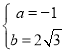 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2+2![]() xЃЛ
xЃЛ
ЃЈ2ЃЉЁпCЃЈ![]() ЃЌ3ЃЉЃЌ
ЃЌ3ЃЉЃЌ
ЁржБЯпOCЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЩшЕуMЕНOCЕФзюДѓОрРыЪБЃЌЦНаагкOCЕФжБЯпНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
СЊСЂ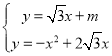 ЃЌ
ЃЌ
ЯћЕєЮДжЊЪ§yВЂећРэЕУЃЌ![]() ЃЌ
ЃЌ
Ёї=ЃЈ![]() ЃЉ2-4m=0ЃЌ
ЃЉ2-4m=0ЃЌ
НтЕУЃКm=![]() ЃЎ
ЃЎ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЁрЕуMЕНOCЕФзюДѓОрРы=![]() ЁСsin30Ёу=
ЁСsin30Ёу=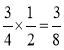 ЃЛ
ЃЛ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ДЫЪБЃЌM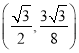 ЃЌзюДѓУцЛ§ЮЊ
ЃЌзюДѓУцЛ§ЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпЁЯOAP=ЁЯBOC=ЁЯBOA =30ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁржБЯпAPгыyжсЕФНЛЕузјБъЮЊЃЈ0ЃЌ2ЃЉЛђЃЈ0ЃЌЉ2ЃЉЃЌ
ЕБжБЯпAPОЙ§ЕуЃЈ![]() ЃЌ0ЃЉЁЂЃЈ0ЃЌ2ЃЉЪБЃЌНтЮіЪНЮЊ
ЃЌ0ЃЉЁЂЃЈ0ЃЌ2ЃЉЪБЃЌНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
СЊСЂ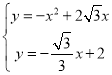 ЃЌ
ЃЌ
НтЕУ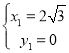 ЃЌ
ЃЌ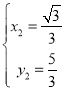 ЃЎ
ЃЎ
ЫљвдЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЕБжБЯпAPОЙ§ЕуЃЈ![]() ЃЌ0ЃЉЁЂЃЈ0ЃЌЉ2ЃЉЪБЃЌНтЮіЪНЮЊ
ЃЌ0ЃЉЁЂЃЈ0ЃЌЉ2ЃЉЪБЃЌНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
СЊСЂ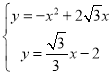
НтЕУ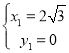 ЃЌ
ЃЌ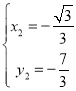 ЃЛ
ЃЛ
ЫљвдЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃЌДцдквЛЕуPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌЪЙЁЯOAP=ЁЯBOAЃЎ
ЃЉЃЌЪЙЁЯOAP=ЁЯBOAЃЎ


 УћЬтН№ОэЯЕСаД№АИ
УћЬтН№ОэЯЕСаД№АИ гХМгОЋОэЯЕСаД№АИ
гХМгОЋОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
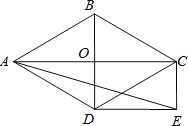
ЁОЬтФПЁПШчЭМ,СтаЮABCDЕФЖдНЧЯпACКЭBDНЛгкЕуO,ЗжБ№Й§ЕуC. DзїCEЁЮBD,DEЁЮACЃЌCEКЭDEНЛгкЕуE.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮODECЪЧОиаЮЃЛ
ЃЈ2ЃЉЕБЁЯADB=60Ёу,AD=2![]() ЪБЃЌЧѓEAЕФГЄЁЃ
ЪБЃЌЧѓEAЕФГЄЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзд2020ФъГѕаТЙкЗЮбзвпЧщБЌЗЂвдРДЃЌЙњФкОМУ--ЖШБЛАДЯТднЭЃМќЃЌШчНёЫцзХЙњФквпЧщЗРПиаЮЪЦГжајЯђКУЃЌИїЕиПЊЪМНјШЫЛ§МЋИДЙЄИДВњЕФаТФЃЪНЃЎФГЩЬМвЮЊНЕЕЭвпЧщДјРДЕФгАЯьЃЌДЬМЄЯћЗбЃЌЮќв§ЙЫПЭЃЌЬиДЫЩшМЦСЫвЛИігЮЯЗЃЌЦфЙцдђЪЧЃКЗжБ№зЊЖЏШчЭМЫљЪОЕФСНИіПЩвдздгЩзЊЖЏЕФзЊХЬИївЛДЮЃЌУПДЮжИеыТфдкУПвЛзжФИЧјгђЕФЛњЛсОљЕШ(ШєжИеыЧЁКУТфдкЗжНчЯпЩЯдђжизЊ)ЃЌЕБСНИізЊХЬЕФжИеыЫљжИзжФИЯрЭЌЪБЃЌЯћЗбепОЭПЩвдЛёЕУвЛДЮАЫелгХЛнМлЙКТђЩЬЦЗЕФЛњЛсЃЎ
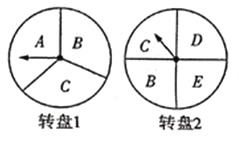
ЃЈ1ЃЉгУЪїзДЭМЛђСаБэЕФЗНЗЈБэЪОГігЮЯЗПЩФмГіЯжЕФЫљгаНсЙћЃЛ
ЃЈ2ЃЉШєаЁССВЮМгвЛДЮгЮЯЗЃЌдђЫћФмЛёЕУАЫелгХЛнМлЙКТђЩЬЦЗЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФКазгРязАга3ИіЗжБ№аДгаЪ§зжЉ2ЃЌ0ЃЌ1ЕФаЁЧђЃЌЫќУЧГ§СЫЪ§зжВЛЭЌвдЭтЦфгрЭъШЋЯрЭЌЃЌЯШДгКазгРяЫцЛњГщШЁ1ИіаЁЧђЃЌдйДгЪЃЯТЕФаЁЧђжаГщШЁ1ИіЃЌНЋетСНИіаЁЧђЩЯЕФЪ§зжвРДЮМЧЮЊaЃЌbЃЌдђТњзуЙигкxЕФЗНГЬx2+ax+bЃН0гаЪЕЪ§ИљЕФИХТЪЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
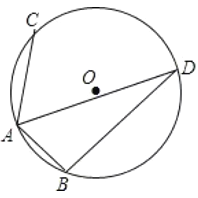
ЁОЬтФПЁПШчЭМЃЌЁбOЕФАыОЖЮЊ4ЃЌAЁЂBЁЂCОљЪЧЁбOЕФЕуЃЌЕуDЪЧЁЯBACЕФЦНЗжЯпгыЁбOЕФНЛЕуЃЌШєЁЯBAC=120ЁуЃЌдђЯвBDЕФГЄЮЊ _____________ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдквЛИіПЩвдздгЩзЊЖЏЕФзЊХЬжаЃЌжИеыЮЛжУЙЬЖЈЃЌШ§ИіЩШаЮЕФУцЛ§ЖМЯрЕШЃЌЧвЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЎ
ЃЈ1ЃЉаЁУїзЊЖЏзЊХЬвЛДЮЃЌЕБзЊХЬЭЃжЙзЊЖЏЪБЃЌжИеыЫљжИЩШаЮжаЕФЪ§зжЪЧЦцЪ§ЕФИХТЪЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉаЁУїЯШзЊЖЏзЊХЬвЛДЮЃЌЕБзЊХЬЭЃжЙзЊЖЏЪБЃЌМЧТМЯТжИеыЫљжИЩШаЮжаЕФЪ§зжЃЛНгзХдйзЊЖЏзЊХЬвЛДЮЃЌЕБзЊХЬЭЃжЙзЊЖЏЪБЃЌдйДЮМЧТМЯТжИеыЫљжИЩШаЮжаЕФЪ§зжЃЌЧѓетСНИіЪ§зжжЎКЭЪЧ3ЕФБЖЪ§ЕФИХТЪЃЈгУЛЪїзДЭМЛђСаБэЕШЗНЗЈЧѓНтЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПТцЭеБЛГЦЮЊЁАЩГФЎжЎжлЁБЃЌЫќЕФЬхЮТЫцЪБМфЕФБфЛЏЖјЗЂЩњНЯДѓБфЛЏЃЌЦфЬхЮТЃЈ![]() ЃЉгыЪБМфЃЈаЁЪБЃЉжЎМфЕФЙиЯЕШчЭМ1ЫљЪОЃЎ
ЃЉгыЪБМфЃЈаЁЪБЃЉжЎМфЕФЙиЯЕШчЭМ1ЫљЪОЃЎ

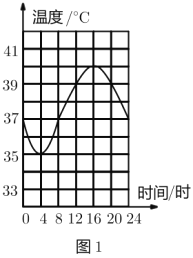
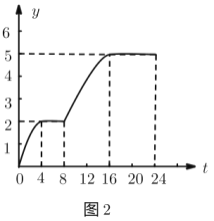
аЁЧхЭЌбЇИљОнЭМ1ЛцжЦСЫЭМ2ЃЌдђЭМ2жаЕФБфСПгаПЩФмБэЪОЕФЪЧЃЈ ЃЉЃЎ
A.ТцЭедк![]() ЪБПЬЕФЬхЮТгы0ЪБЬхЮТЕФОјЖдВюЃЈМДВюЕФОјЖджЕЃЉ
ЪБПЬЕФЬхЮТгы0ЪБЬхЮТЕФОјЖдВюЃЈМДВюЕФОјЖджЕЃЉ
B.ТцЭеДг0ЪБЕН![]() ЪБПЬжЎМфЕФзюИпЬхЮТгыЕБШезюЕЭЬхЮТЕФВю
ЪБПЬжЎМфЕФзюИпЬхЮТгыЕБШезюЕЭЬхЮТЕФВю
C.ТцЭедк![]() ЪБПЬЕФЬхЮТгыЕБШеЦНОљЬхЮТЕФОјЖдВю
ЪБПЬЕФЬхЮТгыЕБШеЦНОљЬхЮТЕФОјЖдВю
D.ТцЭеДг0ЪБЕН![]() ЪБПЬжЎМфЕФЬхЮТзюДѓжЕгызюаЁжЕЕФВю
ЪБПЬжЎМфЕФЬхЮТзюДѓжЕгызюаЁжЕЕФВю
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
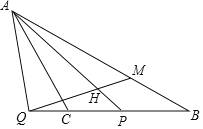
ЁОЬтФПЁПШчЭМЃЌвбжЊЕШбќЁїABCЃЌЁЯACB=120ЁуЃЌPЪЧЯпЖЮCBЩЯвЛЖЏЕуЃЈгыЕуCЃЌBВЛжиКЯЃЉЃЌСЌНгAPЃЌбгГЄBCжСЕуQЃЌЪЙЕУЁЯPAC=ЁЯQACЃЌЙ§ЕуQзїЩфЯпQHНЛЯпЖЮAPгкHЃЌНЛABгкЕуMЃЌЪЙЕУЁЯAHQ=60ЁуЃЎ
ЃЈ1ЃЉШєЁЯPAC=ІСЃЌЧѓЁЯAMQЕФДѓаЁЃЈгУКЌІСЕФЪНзгБэЪОЃЉЃЛ
ЃЈ2ЃЉгУЕШЪНБэЪОЯпЖЮQCКЭBMжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ![]() ИіЕЅЮЛГЄЖШЕФаЁе§ЗНаЮзщГЩЕФ
ИіЕЅЮЛГЄЖШЕФаЁе§ЗНаЮзщГЩЕФ![]() ЕФЭјИёжаЃЌИјГіСЫИёЕу(ЭјИёЯпЕФНЛЕу)ЮЊЖЫЕуЕФЯпЖЮ
ЕФЭјИёжаЃЌИјГіСЫИёЕу(ЭјИёЯпЕФНЛЕу)ЮЊЖЫЕуЕФЯпЖЮ![]()
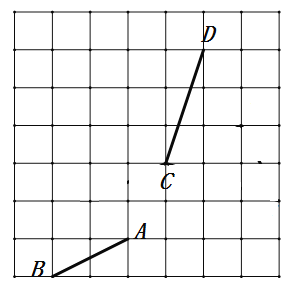
(1)НЋЯпЖЮ![]() ЭЈЙ§ЦНвЦЪЙЕУ
ЭЈЙ§ЦНвЦЪЙЕУ![]() ЕуКЭ
ЕуКЭ![]() ЕужиКЯЃЌ
ЕужиКЯЃЌ![]() ЕуЕФЖдгІЕуЮЊ
ЕуЕФЖдгІЕуЮЊ![]() ЃЌдђгІИУЯШНЋЯпЖЮ
ЃЌдђгІИУЯШНЋЯпЖЮ![]() Яђ ЦНвЦ
Яђ ЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ Иі ЕЅЮЛЃЌЛГі
ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ Иі ЕЅЮЛЃЌЛГі![]() ЦНвЦКѓЖдгІЕФЯпЖЮ
ЦНвЦКѓЖдгІЕФЯпЖЮ![]() ЃЛ
ЃЛ
(2)НЋЯпЖЮ![]() ШЦ
ШЦ![]() ЕуАДЫГЪБеыЗНЯђа§зЊ
ЕуАДЫГЪБеыЗНЯђа§зЊ![]() ЕуЕФЖдгІЕуЮЊ
ЕуЕФЖдгІЕуЮЊ![]() ЃЌЛГіЯпЖЮ
ЃЌЛГіЯпЖЮ![]()
(3)ЬюПеЃК![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com