
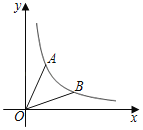
【题目】如图,已知点A(t,1)在第一象限,将OA绕点O顺时针旋转45°得到OB,若反比例数y=![]() (k>0)的图象经过点A、B,则k=_____.
(k>0)的图象经过点A、B,则k=_____.
【答案】![]() ﹣1.
﹣1.
【解析】
根据反比例函数图象关于直线y=x的对称性得,B(1,t),过点A作AC⊥y轴于点C,BE⊥x轴于点E,又由k的几何意义可得k=t,作AO的垂直平分线DE,可得∠CDA=45°,连接AD,根据OC=OD+DC,即1=![]() t+t,进而求出t的值,即为k的值.
t+t,进而求出t的值,即为k的值.
解:如图,点A(t,1),将OA绕点O顺时针旋转45°得到OB,
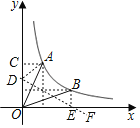
根据反比例函数图象关于直线y=x的对称性得,
B(1,t),
过点A作AC⊥y轴于点C,BE⊥x轴于点E,
又由k的几何意义可知:
k=1×t=t,
∵∠AOB=45°,
∴∠AOC=∠BOE=22.5°,
∴tan∠AOC=tan22.5°=![]() =t=k,
=t=k,
作AO的垂直平分线DF,连接AD,
∴AD=OD,
∴∠DAO=∠DOA=22.5°,
∴∠CDA=45°,
∴DC=CA=t,
∴AD=DO=![]() t,
t,
∴OC=OD+DC,
即1=![]() t+t,
t+t,
解得t=![]() ﹣1.
﹣1.
所以k=![]() ﹣1.
﹣1.
故答案为:![]() ﹣1.
﹣1.


科目:初中数学 来源: 题型:
【题目】移动公司为了提升“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为![]() 的山坡上加装了信号塔
的山坡上加装了信号塔![]() (如图所示),信号塔底端
(如图所示),信号塔底端![]() 到坡底
到坡底![]() 的距离为3.9米.同时为了提醒市民,在距离斜坡底
的距离为3.9米.同时为了提醒市民,在距离斜坡底![]() 点4.4米的水平地面上立了一块警示牌
点4.4米的水平地面上立了一块警示牌![]() .当太阳光线与水平线成
.当太阳光线与水平线成![]() 角时,测得信号塔
角时,测得信号塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 长为3米,则信号塔
长为3米,则信号塔![]() 的高约为(结果精确到十分位,参考数据:
的高约为(结果精确到十分位,参考数据:![]() ,
,![]() ,
,![]() )
)
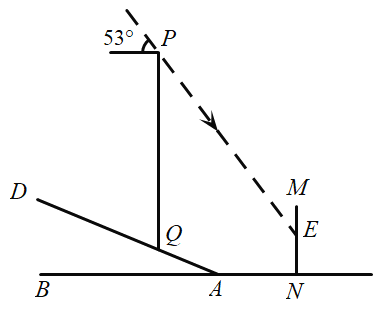
A.11.9米B.10.4米C.11.4米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
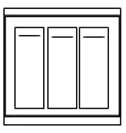
【题目】小惠家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也没有亮).
(1)若小惠任意闭合一个开关,“客厅灯亮了”是_______事件;若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是_______事件(填“不可能”或“必然”或“随机”);
(2)若任意闭合其中两个开关,试用画树状图或列表的方法求“客厅和楼梯灯都亮了”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
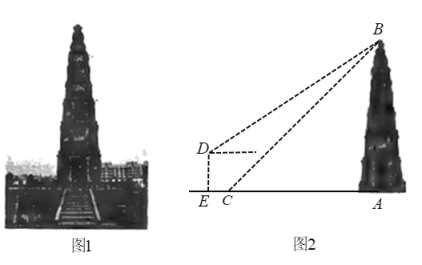
【题目】如图1,在唐河县文峰广场,耸立着一座古老建筑-文峰塔,传说唐河县城是一个船地, 唐中是船头,文峰塔是船的桅杆,无论唐河水怎么涨,唐河县城这艘船也水涨船高.学完了三角函数知识后,某校“数学社团”的刘明和王华决定用自己学到的知识测量文峰塔的高度.如图2,刘明在点![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() 王华在高台上的点
王华在高台上的点![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() ,若高台
,若高台![]() 高为
高为![]() 米,点
米,点![]() 到点
到点![]() 的水平距离EC为
的水平距离EC为![]() 米,且
米,且![]() 三点共线,求该塔
三点共线,求该塔![]() 的高度.(参考数据:
的高度.(参考数据:![]() ,结果保留整数)
,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
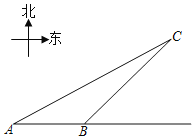
【题目】如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
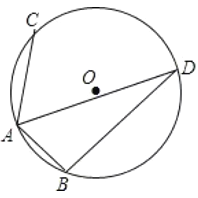
【题目】如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为 _____________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
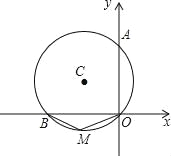
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 到封闭图形
到封闭图形![]() 的“极化距离”
的“极化距离”![]()
![]() 定义如下:任取图形
定义如下:任取图形![]() 上一点
上一点![]() ,记
,记![]() 长度的最大值为
长度的最大值为![]() ,最小值为
,最小值为![]() (若
(若![]() 与
与![]() 重合,则
重合,则![]() ),则“极化距离”
),则“极化距离”![]() .
.

(1)如图1,正方形![]() 以原点
以原点![]() 为中心,点
为中心,点![]() 的坐标为
的坐标为![]() ,
,
①点![]() 到线段
到线段![]() 的“极化距离”
的“极化距离”![]() _______;
_______;
点![]() 到线段
到线段![]() 的“极化距离”
的“极化距离”![]() _________;
_________;
②记正方形![]() 为图形
为图形![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)如图2,图形![]() 为圆心
为圆心![]() 在
在![]() 轴上,半径为
轴上,半径为![]() 的圆,直线
的圆,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 上的任一点
上的任一点![]() 都满足
都满足![]() ,直接写出圆心
,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现2020年全面脱贫的目标,我国实施“精准扶贫”战略,从而使贫困户的生活条件得到改善,生活质量明显提高.为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,统计发现班上贫困家庭学生人数分别有2名,3名,4名,5名,6名,共五种情况.并将其制成了如下两幅不完整的统计图:

请回答下列问题:
(1)求该校一共有班级________个;在扇形统计图中,贫困家庭学生人数有5名的班级所对应扇形圆心角为________°;
(2)将条形图补充完整;
(3)甲、乙、丙是贫困生中的三名学生,学校决定从这三名学生中随机抽取两名代表到市里进行发言,用列表法或画树状图法,求同时抽到甲,乙两名学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com