
【题目】在平面直角坐标系中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,已知
轴上,已知![]() ,抛物线
,抛物线![]() (其中
(其中![]() )经过
)经过![]() 三点,双曲线
三点,双曲线![]() (其中
(其中![]() )经过点
)经过点![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 且
且![]()
(1)求出![]() 的值;当
的值;当![]() 为直角三角形时,请求出
为直角三角形时,请求出![]() 的表达式;
的表达式;
(2)当![]() 为正三角形时,直线
为正三角形时,直线![]() 平分
平分![]() ,求
,求![]() 时
时![]() 的取值范围;
的取值范围;
(3)抛物线![]() (其中
(其中![]() )有一时刻恰好经过
)有一时刻恰好经过![]() 点,且此时抛物线与双曲线
点,且此时抛物线与双曲线![]() (其中
(其中![]() )有且只有一个公共点
)有且只有一个公共点![]() (其中
(其中![]() ),我们不妨把此时刻的
),我们不妨把此时刻的![]() 记作
记作![]() ,请直接写出抛物线
,请直接写出抛物线![]() (其中
(其中![]() )与双曲线
)与双曲线![]() (其中
(其中![]() )有一个公共点时
)有一个公共点时![]() 的取值范围.(
的取值范围.(![]() 是已知数)
是已知数)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题意得![]() ,
,![]() ,故可得出k=
,故可得出k=![]() ;由
;由![]() 变形为
变形为![]() 得A,B两点为抛物线与x轴的交点,故点C为直角顶点,求出点C坐标,代入
得A,B两点为抛物线与x轴的交点,故点C为直角顶点,求出点C坐标,代入![]() ,求出a的值即可;
,求出a的值即可;
(2)由![]() 为正三角形可求出点C坐标,从而得出抛物线y2的解析式,再根据直线
为正三角形可求出点C坐标,从而得出抛物线y2的解析式,再根据直线![]() 平分
平分![]() 求出b和c,得到直线y3解析式,联立y1与y3,y2与y3,求出交点坐标,从而解决问题;
求出b和c,得到直线y3解析式,联立y1与y3,y2与y3,求出交点坐标,从而解决问题;
(3)分![]() 、
、![]() 、
、![]() 、
、![]() ,四种情况分别求解即可.
,四种情况分别求解即可.
(1)∵点![]() 轴,
轴,![]() 轴,
轴,
∴![]() ,
,![]()
又双曲线![]() 经过点
经过点![]()
∴![]() ;
;
∵![]()
∴抛物线y1与x轴的交点坐标为(-1,0),(3,0)
∴点![]() 在抛物线y1上,
在抛物线y1上,
∴点C是直角顶点,AB=3-(-1)=4,
过点C作CD⊥AB于点D,则CD=![]() AB=2,
AB=2,
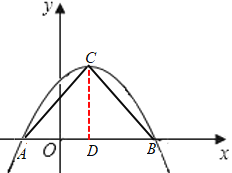
∴OD=AD-AO=1,
∴C(1,2)
把C(1,2)代入![]() ,求得,
,求得,![]()
∴![]()
![]() ;
;
![]() ∵A(-1,0),B(3,0)
∵A(-1,0),B(3,0)
∴AB=4
过C点作CD⊥AB,垂足为D,
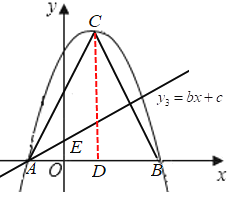
∵△ABC是正三角形,
∴AC=AB=4,AD=![]() AB=2,OD=1
AB=2,OD=1
∴![]()
∴C(1,![]() )
)
把C(1,![]() ) 代入
) 代入![]() ,解得,
,解得,![]() ,
,
∴![]()
∵直线![]() 平分
平分![]() ,
,
∴∠OAE=30°,
∴AE=2OE
∵AO=1,
∴![]() ,解得,
,解得,![]()
∴c=![]()
把(-1,0)代入![]() 得,b=
得,b=![]()
∴![]()
联立![]() 与
与![]() 得
得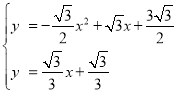
解得,![]() ,
,![]()
所以当![]() 时,
时,![]()
联立![]() 与
与![]() 得
得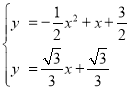 ,
,
解得,![]() ,
,![]()
当![]() 时,
时,![]()
所以当![]() 时,
时,![]()
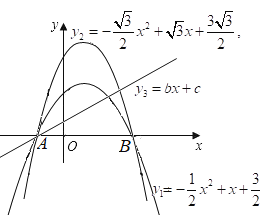
![]() ①当
①当![]() 时,
时,
抛物线![]() 与双曲线
与双曲线![]() 没有公共点;
没有公共点;
②当![]() 时,抛物线
时,抛物线![]() 与双曲线
与双曲线![]() 有唯一公共点
有唯一公共点
③当![]() 时,当抛物线右端点
时,当抛物线右端点![]() 正好落在双曲线上时,
正好落在双曲线上时,![]()
![]() 当
当![]() 时,抛物线
时,抛物线![]() 与双曲线
与双曲线![]() 有两个公共点;
有两个公共点;
④当![]() 时,抛物线
时,抛物线![]() 和双曲线
和双曲线![]() 始终有一个公共点;
始终有一个公共点;
所以当![]() 时,抛物线
时,抛物线![]() 和双曲线
和双曲线![]() 始终有一个公共点
始终有一个公共点


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得![]() ,即
,即![]() ;由周长为m,得
;由周长为m,得![]() ,即
,即![]() .满足要求的
.满足要求的![]() 应是两个函数图象在第 象限内交点的坐标.
应是两个函数图象在第 象限内交点的坐标.
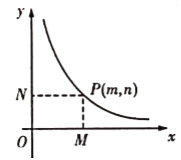
(2)画出函数图象
函数![]() 的图象如图所示,而函数
的图象如图所示,而函数![]() 的图象可由直线
的图象可由直线![]() 平移得到.请在同一直角坐标系中直接画出直线
平移得到.请在同一直角坐标系中直接画出直线![]() .
.
(3)平移直线![]() ,观察函数图象
,观察函数图象
①当直线平移到与函数![]() 的图象有唯一交点
的图象有唯一交点![]() 时,周长m的值为 ;
时,周长m的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
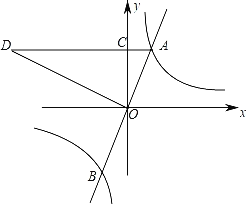
【题目】如图,直线y1=2x与双曲线y2=![]() 交于点A,点B,过点A作AC⊥y轴于点C,OC=2,延长AC至D,使CD=4AC,连接OD.
交于点A,点B,过点A作AC⊥y轴于点C,OC=2,延长AC至D,使CD=4AC,连接OD.
(1)求k的值;
(2)求∠AOD的大小;
(3)直接写出当y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动公司为了提升“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为![]() 的山坡上加装了信号塔
的山坡上加装了信号塔![]() (如图所示),信号塔底端
(如图所示),信号塔底端![]() 到坡底
到坡底![]() 的距离为3.9米.同时为了提醒市民,在距离斜坡底
的距离为3.9米.同时为了提醒市民,在距离斜坡底![]() 点4.4米的水平地面上立了一块警示牌
点4.4米的水平地面上立了一块警示牌![]() .当太阳光线与水平线成
.当太阳光线与水平线成![]() 角时,测得信号塔
角时,测得信号塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 长为3米,则信号塔
长为3米,则信号塔![]() 的高约为(结果精确到十分位,参考数据:
的高约为(结果精确到十分位,参考数据:![]() ,
,![]() ,
,![]() )
)
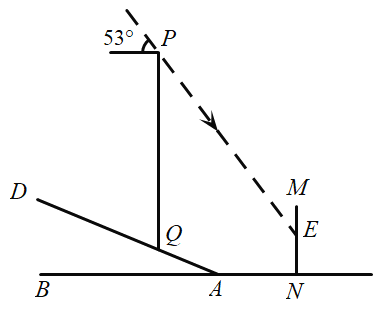
A.11.9米B.10.4米C.11.4米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
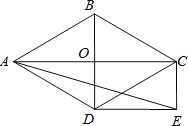
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求EA的长。
时,求EA的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() (
(![]() 是常数,
是常数,![]() )与直线
)与直线![]() 都经过
都经过![]() 轴上的一点
轴上的一点![]() ,且抛物线
,且抛物线![]() 的顶点
的顶点![]() 在直线
在直线![]() 上,则称此直线
上,则称此直线![]() 与该抛物线
与该抛物线![]() 具有“一带一路”关系.此时,直线
具有“一带一路”关系.此时,直线![]() 叫做抛物线
叫做抛物线![]() 的“带线”,抛物线
的“带线”,抛物线![]() 叫做直线
叫做直线![]() 的“路线”.
的“路线”.
(1)若直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,求
具有“一带一路”关系,求![]() 的值;
的值;
(2)若某“路线”![]() 的顶点在反比例函数
的顶点在反比例函数![]() 的图象上,它的“带线”
的图象上,它的“带线”![]() 的解析式为
的解析式为![]() ,求此“路线”
,求此“路线”![]() 的解析式;
的解析式;
(3)当常数![]() 满足
满足![]() 时,请直接写出抛物线
时,请直接写出抛物线![]() :
:![]() 的“带线”
的“带线”![]() 与
与![]() 轴,
轴,![]() 轴所围成的三角形面积S的取值范围.
轴所围成的三角形面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
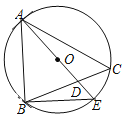
【题目】如图,在△ABC中,∠C=50°,圆O是△ABC的外接圆,AE为圆O的直径,AE与BC相交于点D,若AB=AD.则∠EAC=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
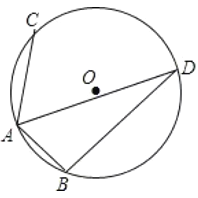
【题目】如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为 _____________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com