
【题目】若抛物线![]() (
(![]() 是常数,
是常数,![]() )与直线
)与直线![]() 都经过
都经过![]() 轴上的一点
轴上的一点![]() ,且抛物线
,且抛物线![]() 的顶点
的顶点![]() 在直线
在直线![]() 上,则称此直线
上,则称此直线![]() 与该抛物线
与该抛物线![]() 具有“一带一路”关系.此时,直线
具有“一带一路”关系.此时,直线![]() 叫做抛物线
叫做抛物线![]() 的“带线”,抛物线
的“带线”,抛物线![]() 叫做直线
叫做直线![]() 的“路线”.
的“路线”.
(1)若直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,求
具有“一带一路”关系,求![]() 的值;
的值;
(2)若某“路线”![]() 的顶点在反比例函数
的顶点在反比例函数![]() 的图象上,它的“带线”
的图象上,它的“带线”![]() 的解析式为
的解析式为![]() ,求此“路线”
,求此“路线”![]() 的解析式;
的解析式;
(3)当常数![]() 满足
满足![]() 时,请直接写出抛物线
时,请直接写出抛物线![]() :
:![]() 的“带线”
的“带线”![]() 与
与![]() 轴,
轴,![]() 轴所围成的三角形面积S的取值范围.
轴所围成的三角形面积S的取值范围.
【答案】(1)p的值为-1,q的值为2;(2)y=![]() x2+2x-1或y= x2+2x-1;(3)
x2+2x-1或y= x2+2x-1;(3)![]() ≤S≤
≤S≤![]() .
.
【解析】
(1)由直线解析式可求出直线与y轴的交点坐标,代入![]() 可求出q值,根据抛物线解析式可求出顶点坐标,代入
可求出q值,根据抛物线解析式可求出顶点坐标,代入![]() 即可求出p值;
即可求出p值;
(2)根据“带线”![]() 解析式可得出直线与y轴的交点坐标为(0,-1),联立“带线”
解析式可得出直线与y轴的交点坐标为(0,-1),联立“带线”![]() 与反比例函数解析式可求出抛物线的顶点坐标为(2,1)或(-1,-2),根据二次函数顶点坐标分别设出解析式,把(0,-1)分别代入即可得答案;
与反比例函数解析式可求出抛物线的顶点坐标为(2,1)或(-1,-2),根据二次函数顶点坐标分别设出解析式,把(0,-1)分别代入即可得答案;
(3)由抛物线解析式可得出抛物线与y轴的交点坐标为(0,k),根据抛物线的解析式可用k表示出其顶点坐标,由两点坐标结合待定系数法即可得出与该抛物线对应的“带线”l的解析式,找出该直线与x、y轴的交点坐标,结合三角形的面积得出面积S关于k的关系式,由二次函数的性质即可得出结论.
(1)令直线y=px+2中x=0,
∴y=2,
∴直线与y轴的交点为(0,2);
∵直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,
具有“一带一路”关系,
∴y=x2-2x+q的图象经过点(0,2),
∴把(0,2)代入y=x2-2x+q得:q=2,
∴抛物线的解析式为y=x2-2x+2=(x-1)2+1,
∴抛物线的顶点坐标为(1,1),
∵直线y=px+2经过抛物线y=x2-2x+q的顶点,
∴1=P+2,
解得:p=-1.
答:p的值为-1,q的值为2.
(2)令“带线”![]() :
:![]() 中x=0得:y=-1,
中x=0得:y=-1,
∴“带线”![]() 与y轴的交点坐标为(0,-1),
与y轴的交点坐标为(0,-1),
联立“带线”![]() 与反比例函数解析式得:
与反比例函数解析式得: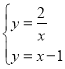 ,
,
解得:![]() ,
,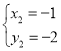 ,
,
∴抛物线的顶点坐标为(2,1)或(-1,-2),
当顶点坐标为(2,1)时,设“路线”![]() 的解析式为y=a(x-2)2+1,
的解析式为y=a(x-2)2+1,
把(0,-1)代入得:-1=4a+1,
解得:a=![]() ,
,
∴“路线”![]() 的解析式为y=
的解析式为y=![]() (x-2)2+1=
(x-2)2+1=![]() x2+2x-1,
x2+2x-1,
当顶点坐标为(-1,-2)时,设“路线”![]() 的解析式为y=a(x+1)2-2,
的解析式为y=a(x+1)2-2,
把(0,-1)代入得:-1=a-2,
解得:a=1,
∴“路线”![]() 的解析式为y=(x+1)2-2=x2+2x-1,
的解析式为y=(x+1)2-2=x2+2x-1,
综上所述:“路线”![]() 的解析式为y=
的解析式为y=![]() x2+2x-1或y= x2+2x-1.
x2+2x-1或y= x2+2x-1.
(3)令抛物线![]() :
:![]() 中x=0得:y=k,
中x=0得:y=k,
∴该抛物线与y轴的交点为(0,k),
∵抛物线![]() 的解析式为
的解析式为![]() ,
,
∴顶点坐标为[![]() ,
,![]() ],
],
设“带线”![]() 的解析式为y=mx+k,
的解析式为y=mx+k,
∵点[![]() ,
,![]() ]在y=mx+k图象上,
]在y=mx+k图象上,
∴![]() =m[
=m[![]() ]+k,
]+k,
解得:m=![]() ,
,
∴“带线”![]() 的解析式为y=
的解析式为y=![]() x+k,
x+k,
令“带线”![]() :y=
:y=![]() x+k中y=0得:
x+k中y=0得:![]() x+k=0,
x+k=0,
解得:x=![]() ,
,
∴“带线”![]() 与x轴得交点为(
与x轴得交点为(![]() ,0),与y轴交点坐标为(0,k),
,0),与y轴交点坐标为(0,k),
∴S=![]() |
|![]() ||k|,
||k|,
∵![]() ,
,
∴![]() ,
,
∴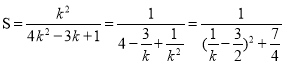 ,
,
∴当![]() 时,S有最大值为
时,S有最大值为![]() ,
,
∵|![]() |<|
|<|![]() -4|,
-4|,
∴当![]() 时,
时,![]() 时,
时,![]() 取最大值
取最大值![]() ,
,
∴![]() 时,S有最小值
时,S有最小值![]() ,
,
∴S的取值范围为![]() ≤S≤
≤S≤![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
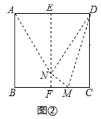
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
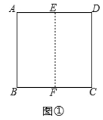
折一折:把边长为4的正方形纸片![]() 对折,使边
对折,使边![]() 与
与![]() 重合,展开后得到折痕
重合,展开后得到折痕![]() .如图①:
.如图①:![]() 为
为![]() 上一点,将正方形纸片
上一点,将正方形纸片![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 的点
的点![]() 处,展开后连接
处,展开后连接![]() ,如图②
,如图②
(一)做一做:
(1)图②中,求![]() 的度数和线段
的度数和线段![]() 的长度.
的长度.
(2)图②中,试判断![]() 的形状,并给出证明.
的形状,并给出证明.
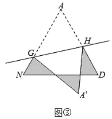
剪一剪、折一折:将图②中的![]() 剪下来,将其沿直线
剪下来,将其沿直线![]() 折叠,使点
折叠,使点![]() 落在点
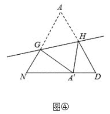
落在点![]() 处,分别得到图③、图④.
处,分别得到图③、图④.
(二)填一填:
(3)图③中阴影部分的周长为________.
(4)图③中,若![]() ,则
,则![]() __________
__________![]() .
.
(5)如图④点![]() 落在边
落在边![]() 上,若
上,若![]() ,则
,则![]() ______(用含
______(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 的直角边于点
的直角边于点![]() ,以
,以![]() 为边向
为边向![]() 右侧作正方形
右侧作正方形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒,正方形
秒,正方形![]() 与
与![]() 的重叠部分的面积为
的重叠部分的面积为![]() .
.
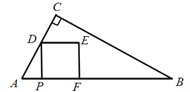
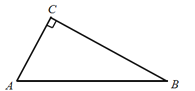
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,已知
轴上,已知![]() ,抛物线
,抛物线![]() (其中
(其中![]() )经过
)经过![]() 三点,双曲线
三点,双曲线![]() (其中
(其中![]() )经过点
)经过点![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 且
且![]()
(1)求出![]() 的值;当
的值;当![]() 为直角三角形时,请求出
为直角三角形时,请求出![]() 的表达式;
的表达式;
(2)当![]() 为正三角形时,直线
为正三角形时,直线![]() 平分
平分![]() ,求
,求![]() 时
时![]() 的取值范围;
的取值范围;
(3)抛物线![]() (其中
(其中![]() )有一时刻恰好经过
)有一时刻恰好经过![]() 点,且此时抛物线与双曲线
点,且此时抛物线与双曲线![]() (其中
(其中![]() )有且只有一个公共点
)有且只有一个公共点![]() (其中
(其中![]() ),我们不妨把此时刻的
),我们不妨把此时刻的![]() 记作
记作![]() ,请直接写出抛物线
,请直接写出抛物线![]() (其中
(其中![]() )与双曲线
)与双曲线![]() (其中
(其中![]() )有一个公共点时
)有一个公共点时![]() 的取值范围.(
的取值范围.(![]() 是已知数)
是已知数)
查看答案和解析>>
科目:初中数学 来源: 题型:
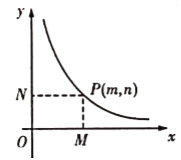
【题目】在平面直角坐标系![]() 中,A(-4,3),B(0,1),将线段AB沿
中,A(-4,3),B(0,1),将线段AB沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数
个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数![]() 的图象上.
的图象上.
(1)用含![]() 的代数式表示点A′,B′的坐标;
的代数式表示点A′,B′的坐标;
(2)求![]() 的值和反比例函数
的值和反比例函数![]() 的表达式;
的表达式;
(3)点![]() 为反比例函数
为反比例函数![]() 图象上的一个动点,直线
图象上的一个动点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,请直接写出点C的坐标.
,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() .
.
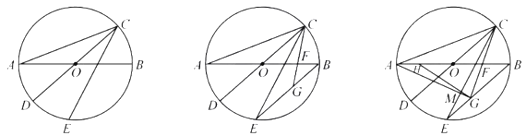
(1)求证:![]() 平分
平分![]() ;
;
(2)如图2,连接![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.

(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某个函数,若自变量取实数![]() ,其函数值恰好也等于
,其函数值恰好也等于![]() 时,则称
时,则称![]() 为这个函数的“等量值”.在函数存在“等量值”时,该函数的最大“等量值”与最小“等量值”的差
为这个函数的“等量值”.在函数存在“等量值”时,该函数的最大“等量值”与最小“等量值”的差![]() 称为这个函数的“等量距离”,特别地,当函数只有一个“等量值”时,规定其“等最距离”
称为这个函数的“等量距离”,特别地,当函数只有一个“等量值”时,规定其“等最距离”![]() 为0.
为0.
(1)请分别判断函数![]() ,
,![]() ,
,![]() 有没有“等量值”?如果有,直接写出其“等量距离”;
有没有“等量值”?如果有,直接写出其“等量距离”;
(2)已知函数![]() .
.
①若其“等量距离”为0,求![]() 的值;
的值;
②若![]() ,求其“等量距离”
,求其“等量距离”![]() 的取值范围;
的取值范围;
③若“等量距离”![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚筒轮⊙A,⊙A与水平地面相切于点D,在拉杆伸长到最大的情况下,当点B距离水平地面34cm时,点C到水平地面的距离CE为55cm.设AF∥ MN.
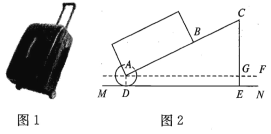
(1)求⊙A的半径.
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果精确到1cm,参考数据:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com