
【题目】在平面直角坐标系![]() 中,A(-4,3),B(0,1),将线段AB沿
中,A(-4,3),B(0,1),将线段AB沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数
个单位,得到线段A′B′,且A′,B′恰好都落在反比例函数![]() 的图象上.
的图象上.
(1)用含![]() 的代数式表示点A′,B′的坐标;
的代数式表示点A′,B′的坐标;
(2)求![]() 的值和反比例函数
的值和反比例函数![]() 的表达式;
的表达式;
(3)点![]() 为反比例函数
为反比例函数![]() 图象上的一个动点,直线
图象上的一个动点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,请直接写出点C的坐标.
,请直接写出点C的坐标.
【答案】(1)A′(-4+n,3),B′(n,1);(2)n的值为6,反比例函数解析式为![]() ;(3)点C坐标为(
;(3)点C坐标为(![]() ,9)或(-
,9)或(-![]() ,-9).
,-9).
【解析】
(1)根据平移的性质即可得答案;
(2)把A′、B′坐标代入![]() 可得关于m、n的方程组,解方程组求出m、n的值即可得答案;
可得关于m、n的方程组,解方程组求出m、n的值即可得答案;
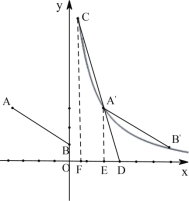
(3)①当点C在第一象限时,如图,过A′作A′E⊥x轴于E,过C作CF⊥x轴于F,可知AE′//CF,可得![]() ,可求出CF的出,可得点C纵坐标,代入反比例函数解析式即可求出点C横坐标;②当点C在第三象限时,如图,同理可求出CF的长及点C横坐标;综上即可得答案.
,可求出CF的出,可得点C纵坐标,代入反比例函数解析式即可求出点C横坐标;②当点C在第三象限时,如图,同理可求出CF的长及点C横坐标;综上即可得答案.
(1)∵线段AB沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位,A(-4,3),B(0,1),
个单位,A(-4,3),B(0,1),
∴A′(-4+n,3),B′(n,1).
(2)∵A′,B′恰好都落在反比例函数![]() 的图象上,
的图象上,
∴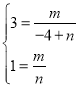 ,
,
解得:![]() ,
,
∴n的值为6,反比例函数解析式为![]() .
.
(3)①当点C在第一象限时,如图,过A′作A′E⊥x轴于E,过C作CF⊥x轴于F,
∴AE′//CF,
∴![]() ,
,
∵A′(2,3),
∴A′E=3,
∵![]() ,
,
∴CF=9,
∴点C纵坐标为9,
∵点C在反比例函数![]() 图象上,
图象上,
∴9=![]() ,
,
解得:x=![]() ,
,
∴点C坐标为(![]() ,9).
,9).
②当点C在第三象限时,如图,过A′作A′E⊥x轴于E,过C作CF⊥x轴于F,
同①可得:CF=9,
∵点C在第三象限,
∴点C纵坐标为-9,
∵点C在反比例函数![]() 图象上,
图象上,
∴-9=![]() ,
,
解得:x=-![]() ,
,
∴点C坐标为(-![]() ,-9).
,-9).

综上所述:点C坐标为(![]() ,9)或(-
,9)或(-![]() ,-9).
,-9).


科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
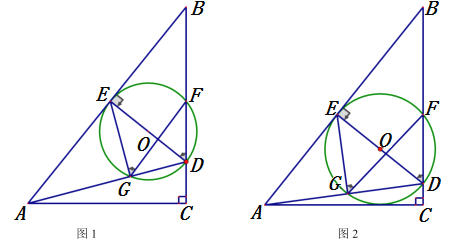
【题目】如图1,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一个动点,作
上一个动点,作![]() ,交直角边
,交直角边![]() 于点
于点![]() ,以
,以![]() 为直径作
为直径作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 交
交![]() 于点
于点![]() .连结
.连结![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(2)求证:![]() ;
;
(3)如图2,当![]() 与边
与边![]() 相切时,求
相切时,求![]() 的直径;
的直径;
(4)若以![]() 为顶点的三角形是等腰三角形时,求所有满足条件的
为顶点的三角形是等腰三角形时,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
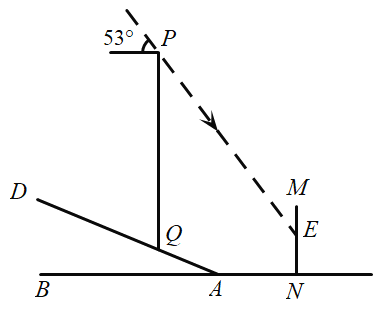
【题目】移动公司为了提升“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为![]() 的山坡上加装了信号塔
的山坡上加装了信号塔![]() (如图所示),信号塔底端
(如图所示),信号塔底端![]() 到坡底
到坡底![]() 的距离为3.9米.同时为了提醒市民,在距离斜坡底
的距离为3.9米.同时为了提醒市民,在距离斜坡底![]() 点4.4米的水平地面上立了一块警示牌
点4.4米的水平地面上立了一块警示牌![]() .当太阳光线与水平线成
.当太阳光线与水平线成![]() 角时,测得信号塔
角时,测得信号塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 长为3米,则信号塔
长为3米,则信号塔![]() 的高约为(结果精确到十分位,参考数据:
的高约为(结果精确到十分位,参考数据:![]() ,
,![]() ,
,![]() )
)
A.11.9米B.10.4米C.11.4米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() (
(![]() 是常数,
是常数,![]() )与直线
)与直线![]() 都经过
都经过![]() 轴上的一点
轴上的一点![]() ,且抛物线
,且抛物线![]() 的顶点
的顶点![]() 在直线
在直线![]() 上,则称此直线
上,则称此直线![]() 与该抛物线
与该抛物线![]() 具有“一带一路”关系.此时,直线
具有“一带一路”关系.此时,直线![]() 叫做抛物线
叫做抛物线![]() 的“带线”,抛物线
的“带线”,抛物线![]() 叫做直线
叫做直线![]() 的“路线”.
的“路线”.
(1)若直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,求
具有“一带一路”关系,求![]() 的值;
的值;
(2)若某“路线”![]() 的顶点在反比例函数
的顶点在反比例函数![]() 的图象上,它的“带线”
的图象上,它的“带线”![]() 的解析式为
的解析式为![]() ,求此“路线”
,求此“路线”![]() 的解析式;
的解析式;
(3)当常数![]() 满足
满足![]() 时,请直接写出抛物线
时,请直接写出抛物线![]() :
:![]() 的“带线”
的“带线”![]() 与
与![]() 轴,
轴,![]() 轴所围成的三角形面积S的取值范围.
轴所围成的三角形面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
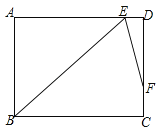
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
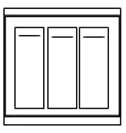
【题目】小惠家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也没有亮).
(1)若小惠任意闭合一个开关,“客厅灯亮了”是_______事件;若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是_______事件(填“不可能”或“必然”或“随机”);
(2)若任意闭合其中两个开关,试用画树状图或列表的方法求“客厅和楼梯灯都亮了”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
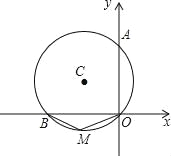
【题目】如图,⊙C 经过原点且与两坐标轴分别交于点 A 与点 B,点 B 的坐标为(﹣![]() ,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
,0),M 是圆上一点,∠BMO=120°.⊙C 圆心 C 的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com