
【题目】已知:点M、P、N、Q依次是正方形ABCD的边AB、BC、CD、DA上一点(不与正方形的顶点重合),给出如下结论:
①MN⊥PQ,则MN=PQ;
②MN=PQ,则MN⊥PQ;
③△AMQ≌△CNP,则△BMP≌△DNQ;
④△AMQ∽△CNP,则△BMP∽△DNQ
其中所有正确的结论的序号是 .
【答案】①②③
【解析】解:连接QM,MP,PN,PQ,过N作NE⊥AB于E,过Q作QF⊥BC于F,
则四边形BCNE,四边形CDQF是矩形,
∴EN=BC,QF=CD,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,
∴NE=QF,
①∵MN⊥PQ,
∴∠PQF=∠MNE,
在△PQF与△MNE中, 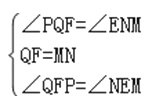 ,
,
∴△PQF≌△MNE,
∴MN=PQ;
②在Rt△PQF与Rt△MNE中, 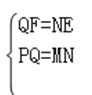 ,
,
∴Rt△PQF≌Rt△MNE,
∴∠PQF=∠MNE,
∵∠PQF+∠1=90°,
∴∠MNE+∠1=90°,
∴MN⊥PQ;
③∵△AMQ≌△CNP,
∴AM=CN,PC=AQ,
∴PB=QD,BM=DN,
在△BMP与△DNQ中, 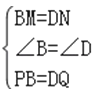 ,
,
∴△BMP≌△DNQ,
④由△AMQ∽△CNP和已知条件推不出△BMP∽△DNQ的条件.
所以答案是:①②③.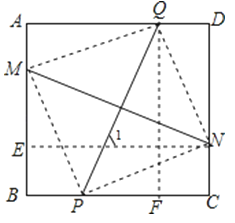


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=52°,点P是射线AM上的动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校假期由校长带领该校“三好学生”去旅游,甲旅行社说“若校长买全票一张,则学生半价.”乙旅行社说“全部人六折优惠”若全票价是1200元,则:
(1)若学生人数是20人,甲、乙旅行社收费分别是多少?
(2)当学生人数的多少时,两家旅行社的收费一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3,BC=5,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.
(1)求证:四边形CEDF是平行四边形;
(2)① 当AE= 时,四边形CEDF是矩形;
② 当AE= 时,四边形CEDF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,O为坐标原点,横、纵轴的单位长度相同,A、B的坐标分别为(8,6),(16,0),点P沿OA边从点O开始向终点A运动,速度每秒1个单位,点Q沿BO边从B点开始向终点O运动,速度每秒2个单位,如果P、Q同时出发,用t(秒)表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动。求:

(1)几秒时PQ∥AB.
(2)设△OPQ的面积为y,求y与t的函数关系式.
(3)△OPQ与△OAB能否相似?若能,求出点P的坐标,若不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)作出将△ABC绕原点O按逆时针方向旋转90°后所得的△A2B2C2;
(3)写出点A1、A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.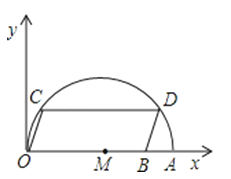
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x-1,令y=0可得x=1,我们就说1是函数y=x-1的零点.
已知y=x2-2mx-2(m+3)(m为常数).
(1)当m=0时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为x1和x2,且![]() ,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 筐葡萄,以每筐
筐葡萄,以每筐![]() 千克为标准,超过或不足的千克数分别用正、负数来表示,与标准质量的差值记录如下:
千克为标准,超过或不足的千克数分别用正、负数来表示,与标准质量的差值记录如下:
单位(千克) |
|
|
|
|
|
|
筐数 |
|
|
|
|
|
|
(1)![]() 筐葡萄中,最重的一筐比最轻的一筐重________千克.
筐葡萄中,最重的一筐比最轻的一筐重________千克.
(2)与标准重量比较,![]() 筐葡萄总计超过或不足多少千克?
筐葡萄总计超过或不足多少千克?
(3)若葡萄每千克售价![]() 元,则出售这
元,则出售这![]() 筐葡萄可卖多少元?
筐葡萄可卖多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com