
【题目】已知二次函数y=ax2-4x+c,函数值y与自变量x之间的部分对应值如表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 15 | m | n | 0 | k | … |
(1)求这个二次函数的关系式.
(2)直接写出m、n、k之间的大小关系.(用“>”连接)
(3)若点P在这个二次函数的图象上,且点P到x轴的距离为1,求点P的坐标.
【答案】(1)这个二次函数的关系式为y=x2-4x+3;(2)m>n>k;(3)P点坐标为(2+![]() ,1),(2-
,1),(2-![]() ,1),(2,-1)
,1),(2,-1)
【解析】
(1)利用待定系数法求抛物线解析式; (2)先确定抛物线的对称轴,然后根据二次函数的性质判断m、n、k之间的大小关系; (3)计算函数值为1或-1对应的自变量的值即可得到P点坐标.
(1)把(-2,15),(1,0)代入y=ax2-4x+c得![]() ,解得
,解得![]() ,
,
∴这个二次函数的关系式为y=x2-4x+3;
(2)∵抛物线的对称轴为直线x=2,
∴m>n>k;
(3)∵点P到x轴的距离为1,
∴P点的纵坐标为1或-1,
当y=1时,x2-4x+3=1,解得x1=2+![]() ,x2=2-
,x2=2-![]() ;
;
当y=-1时,x2-4x+3=-1,解得x1=x2=2;
∴P点坐标为(2+![]() ,1),(2-
,1),(2-![]() ,1),(2,-1).
,1),(2,-1).


科目:初中数学 来源: 题型:
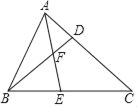
【题目】如图,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CDCA=CECB.
(1)求证:∠CAE=∠CBD;
(2)若![]() ,求证:ABAD=AFAE.
,求证:ABAD=AFAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
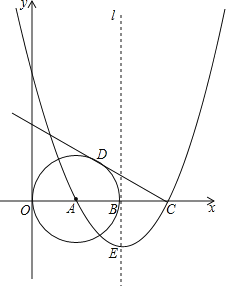
【题目】如图,已知点A(2,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A,抛物线与x轴的另一个交点为点C,抛物线的顶点为点E,如果CO=2BE,求此抛物线的解析式;
(2)过点C作⊙A的切线CD,D为切点,求此切线长;
(3)点F是切线CD上的一个动点,当△BFC与△CAD相似时,求出BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
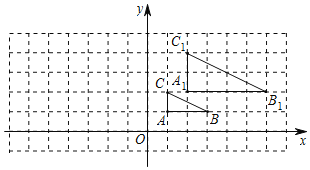
【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
(1)△A1B1C1与△ABC的位似比是______.
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
(3)若点B的坐标为(3,1)为△ABC内一点,则依上述两次变换后,点B2的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形组成的![]() 网格,直线
网格,直线![]() 是一条网格线,点
是一条网格线,点![]() ,
,![]() 在格点上,
在格点上,![]() 的三个顶点都在格点(网格线的交点)上.
的三个顶点都在格点(网格线的交点)上.

(1)作出![]() 关于直线
关于直线![]() 对称的
对称的![]() ;
;
(2)在直线![]() 上画出点
上画出点![]() ,使四边形
,使四边形![]() 的周长最小;
的周长最小;
(3)在这个![]() 网格中,到点
网格中,到点![]() 和点
和点![]() 的距离相等的格点有_________个.
的距离相等的格点有_________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
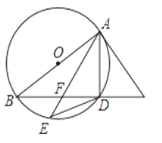
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com