
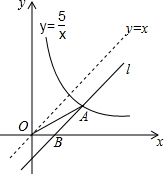
 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )
如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )| A. | 5 | B. | 10 | C. | 15 | D. | 25 |
分析 平移后解析式是y=x-b,代入y=$\frac{5}{x}$求出x2+bx=5,y=x-b与x轴交点B的坐标是(b,0),设A的坐标是(x,y),求出OA2-OB2=x2+(x-b)2-b2=2(x2-xb),代入求出即可.
解答 解:∵平移后解析式是y=x-b,
代入y=$\frac{5}{x}$得:x-b=$\frac{5}{x}$,
即x2-bx=5,
y=x-b与x轴交点B的坐标是(b,0),
设A的坐标是(x,y),
∴OA2-OB2
=x2+y2-b2
=x2+(x-b)2-b2
=2x2-2xb
=2(x2-xb)
=2×5=10,
故选B.
点评 本题考查了一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力的能力.


科目:初中数学 来源: 题型:选择题
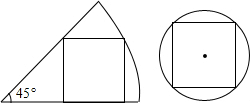 把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )
把一张圆形纸片和一张含45°角的扇形纸片如图所示的方式分别剪得一个正方形,如果所剪得的两个正方形边长都是1,那么圆形纸片和扇形纸片的面积比是( )| A. | 4:5 | B. | 2:5 | C. | $\sqrt{5}$:2 | D. | $\sqrt{5}$:$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在装满红球的箱子里摸出一个白球是不确定事件 | |
| B. | 想了解重庆市民的幸福指数,宜采取抽样调查 | |
| C. | 某种福利彩票的中奖概率为$\frac{1}{10000}$,说明每买10000张彩票,一定有一张中奖 | |
| D. | 抛掷一枚图钉,钉尖朝上的概率是$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com