
分析 首先由二次函数的最值问题,求得-2<m≤2;又由关于x方程mx2+x-2=0有解,求得m的取值范围,继而求得m=1或2,再利用概率公式即可求得答案.
解答 解:∵使二次函数y=-$\frac{1}{4}(x+2)^{2}+3$的最大值3,
即当x=-2时,y取最大值3,
∴m>-2,
∵使二次函数y=-$\frac{1}{4}(x+2)^{2}+3$在-6≤x<m时有最小值-1,
∴-$\frac{1}{4}(x+2)^{2}+3$=-1,
解得:x1=2,x2=-6,
∴m≤2,
∴当-2<m≤2时,使二次函数y=-$\frac{1}{4}(x+2)^{2}+3$在-6≤x<m时有最小值-1,最大值3;
∵关于x方程mx2+x-2=0有解,
∴△=1-4×m×(-2)=8m+1≥0,
解得:m≥-$\frac{1}{8}$,
综上,-$\frac{1}{8}$≤m≤2,
∴m=1,2,
∴使二次函数y=-$\frac{1}{4}(x+2)^{2}+3$在-6≤x<m时有最小值-1,最大值3,且关于x方程mx2+x-2=0有解的概率为:$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了概率公式的应用、二次函数的最值以及一元二次方程的根的判别式.用到的知识点为:概率=所求情况数与总情况数之比.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 晴天的早晨,太阳从东方升起 | |
| B. | 测量某天的最低气温,结果为-150℃ | |
| C. | 打开数学课本时刚好翻到第60页 | |
| D. | 在一次体育考试中,小王跑100米用了4秒钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | $\sqrt{3}$ | C. | $\frac{3}{16}$ | D. | -0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
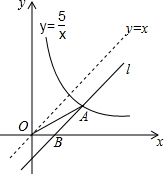 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )
如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y=$\frac{5}{x}$(x>0)的图象相交于点A,与x轴相交于点B,则OA2-OB2的值为( )| A. | 5 | B. | 10 | C. | 15 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
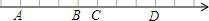 已知:如图,A,B,C,D四点对应的实数都是整数,若点A对应于实数a,点B对应于实数b,点C对应于实数c,数轴上每个小格对应一个单位长度且c-2b=5,那么数轴上的原点应是( )点.
已知:如图,A,B,C,D四点对应的实数都是整数,若点A对应于实数a,点B对应于实数b,点C对应于实数c,数轴上每个小格对应一个单位长度且c-2b=5,那么数轴上的原点应是( )点.| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
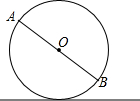 如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.
如图,⊙O沿直线l滚动.已知⊙O的半径是0.4m,AB是⊙O的一条直径,当⊙O沿地面滚动时,点A,B到l的距离之和是否改变?若改变,请说明理由;若不改变,请求出点A,B到l的距离之和.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com