
分析 根据二次根式和分式有意义的条件可得$\left\{\begin{array}{l}{x-3≥0}\\{x-2>0}\end{array}\right.$或$\left\{\begin{array}{l}{x-3≤0}\\{x-2<0}\end{array}\right.$,再分别计算出两个不等式组的解集即可.
解答 解:由题意得:$\left\{\begin{array}{l}{x-3≥0}\\{x-2>0}\end{array}\right.$或$\left\{\begin{array}{l}{x-3≤0}\\{x-2<0}\end{array}\right.$,
解得:x≥3或x<2,
故答案为:x≥3或x<2.
点评 此题主要考查了二次根式和分式有意义的条件,分式有意义,分母不为0;二次根式的被开方数是非负数.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案科目:初中数学 来源: 题型:选择题
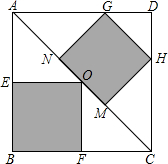 如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟不落在花圃上的概率为( )| A. | $\frac{19}{36}$ | B. | $\frac{1}{2}$ | C. | $\frac{17}{36}$ | D. | $\frac{17}{32}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
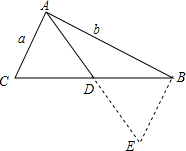 如图所示,在三角形中已知两边之长分别为a,b(a<b),那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$<x<$\frac{b+a}{2}$.
如图所示,在三角形中已知两边之长分别为a,b(a<b),那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$<x<$\frac{b+a}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
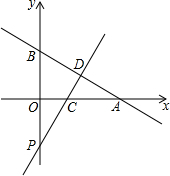 如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,将△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D.
如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,将△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com