
ΓΨΧβΡΩΓΩ‘ΡΕΝάμΫβΘΚ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Ε‘”Ύ»Έ“βΝΫΒψ
÷–Θ§Ε‘”Ύ»Έ“βΝΫΒψ![]() ”κ
”κ![]() ΒΡΓΑΖ«≥ΘΨύάκΓ±Ηχ≥ωœ¬Ν–Ε®“εΘΚ »τ
ΒΡΓΑΖ«≥ΘΨύάκΓ±Ηχ≥ωœ¬Ν–Ε®“εΘΚ »τ![]() Θ§‘ρΒψ
Θ§‘ρΒψ![]() ”κ
”κ![]() ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ
ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ![]() ΘΜ
ΘΜ
»τ![]() Θ§‘ρΒψ
Θ§‘ρΒψ![]() ”κ
”κ![]() ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ
ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ![]() . άΐ»γΘΚΒψ
. άΐ»γΘΚΒψ![]() Θ§Βψ
Θ§Βψ![]() Θ§“ρΈΣ
Θ§“ρΈΣ![]() Θ§Υυ“‘Βψ
Θ§Υυ“‘Βψ![]() ”κ
”κ![]() ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ
ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ![]() Θ§“≤ΨΆ «ΆΦ1÷–œΏΕΈ
Θ§“≤ΨΆ «ΆΦ1÷–œΏΕΈ![]() ”κœΏΕΈ
”κœΏΕΈ![]() ≥ΛΕ»ΒΡΫœ¥σ÷ΒΘ®ΒψQΈΣ¥Ι÷±”Ύ
≥ΛΕ»ΒΡΫœ¥σ÷ΒΘ®ΒψQΈΣ¥Ι÷±”Ύ![]() ÷αΒΡ÷±œΏ
÷αΒΡ÷±œΏ![]() ”κ¥Ι÷±”Ύ
”κ¥Ι÷±”Ύ![]() ÷αΒΡ÷±œΏ
÷αΒΡ÷±œΏ![]() ΒΡΫΜΒψΘ©Θ°
ΒΡΫΜΒψΘ©Θ°
Θ®1Θ©“―÷ΣΒψA![]() Θ§BΈΣ
Θ§BΈΣ![]() ÷α…œ“ΜΗωΕ·ΒψΘ°
÷α…œ“ΜΗωΕ·ΒψΘ°
ΔΌ»τΒψBΘ®0Θ§3Θ©Θ§‘ρΒψA”κΒψBΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ ΘΜ
ΔΎ»τΒψA”κΒψBΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ2Θ§‘ρΒψBΒΡΉχ±ξΈΣ ΘΜ
Δέ÷±Ϋ”–¥≥ωΒψA”κΒψBΒΡΓΑΖ«≥ΘΨύάκΓ±ΒΡΉν–Γ÷Β .
Θ®2Θ©“―÷ΣΒψDΘ®0Θ§1Θ©ΒψC «÷±œΏ![]() …œΒΡ“ΜΗωΕ·ΒψΘ§»γΆΦ2Θ§«σΒψC”κΒψDΓΑΖ«≥ΘΨύάκΓ±ΒΡΉν–Γ÷ΒΦΑœύ”ΠΒΡΒψCΒΡΉχ±ξ.
…œΒΡ“ΜΗωΕ·ΒψΘ§»γΆΦ2Θ§«σΒψC”κΒψDΓΑΖ«≥ΘΨύάκΓ±ΒΡΉν–Γ÷ΒΦΑœύ”ΠΒΡΒψCΒΡΉχ±ξ.
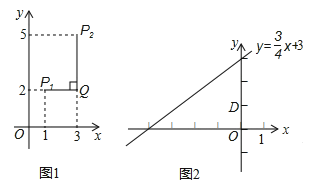
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ3Θ§ΔΎΘ®0Θ§2Θ©ΜρΘ®0Θ§Θ≠2Θ© Δέ![]() Θ®2Θ©
Θ®2Θ©![]()
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΔΌΗυΨί»τ|x1-x2|ΘΦ|y1-y2|Θ§‘ρΒψP1”κΒψP2ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ|y1-y2|Ϋβ¥πΦ¥Ω…ΘΜ
ΔΎΗυΨίΒψBΈΜ”Ύy÷α…œΘ§Ω…“‘…ηΒψBΒΡΉχ±ξΈΣΘ®0Θ§yΘ©Θ°”…ΓΑΖ«≥ΘΨύάκΓ±ΒΡΕ®“εΩ…“‘»ΖΕ®|0-y|=2Θ§Ψί¥ΥΩ…“‘«σΒΟyΒΡ÷ΒΘΜ
Δέ…ηΒψBΒΡΉχ±ξΈΣΘ®0Θ§yΘ©Θ°“ρΈΣ|-![]() -0|Γί|0-y|Θ§Υυ“‘ΒψA”κΒψBΒΡΓΑΖ«≥ΘΨύάκΓ±Ήν–Γ÷ΒΈΣ|-
-0|Γί|0-y|Θ§Υυ“‘ΒψA”κΒψBΒΡΓΑΖ«≥ΘΨύάκΓ±Ήν–Γ÷ΒΈΣ|-![]() -0|=
-0|=![]() ΘΜ
ΘΜ
Θ®2Θ©…ηΒψCΒΡΉχ±ξΈΣΘ®x0Θ§ ![]() x0+3Θ©Θ°ΗυΨί≤ΡΝœΓΑ»τ|x1-x2|Γί|y1-y2|Θ§‘ρΒψP1”κΒψP2ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ|x1-x2|Γ±÷ΣΘ§CΓΔDΝΫΒψΒΡΓΑΖ«≥ΘΨύάκΓ±ΒΡΉν–Γ÷ΒΈΣ-x0=
x0+3Θ©Θ°ΗυΨί≤ΡΝœΓΑ»τ|x1-x2|Γί|y1-y2|Θ§‘ρΒψP1”κΒψP2ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ|x1-x2|Γ±÷ΣΘ§CΓΔDΝΫΒψΒΡΓΑΖ«≥ΘΨύάκΓ±ΒΡΉν–Γ÷ΒΈΣ-x0=![]() x0+2Θ§Ψί¥ΥΩ…“‘«σΒΟΒψCΒΡΉχ±ξΘ°
x0+2Θ§Ψί¥ΥΩ…“‘«σΒΟΒψCΒΡΉχ±ξΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏ|-![]() -0|=
-0|=![]() Θ§|0-3|=3Θ§
Θ§|0-3|=3Θ§
Γύ![]() ΘΦ3Θ§
ΘΦ3Θ§
ΓύΒψA”κΒψBΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ3Θ°
ΔΎΓΏBΈΣy÷α…œΒΡ“ΜΗωΕ·ΒψΘ§
Γύ…ηΒψBΒΡΉχ±ξΈΣΘ®0Θ§yΘ©Θ°
ΓΏ|-![]() -0|=
-0|=![]() ΓΌ2Θ§
ΓΌ2Θ§
Γύ|0-y|=2Θ§
ΫβΒΟΘ§y=2Μρy=-2ΘΜ
ΓύΒψBΒΡΉχ±ξ «Θ®0Θ§2Θ©ΜρΘ®0Θ§-2Θ©Θ§
ΔέΒψA”κΒψBΒΡΓΑΖ«≥ΘΨύάκΓ±ΒΡΉν–Γ÷ΒΈΣ![]() Θ°
Θ°
Θ®2Θ©»γΆΦ2Θ§»ΓΒψC”κΒψDΒΡΓΑΖ«≥ΘΨύάκΓ±ΒΡΉν–Γ÷Β ±Θ§

–η“ΣΗυΨί‘ΥΥψΕ®“εΓΑ»τ|x1-x2|Γί|y1-y2|Θ§‘ρΒψP1”κΒψP2ΒΡΓΑΖ«≥ΘΨύάκΓ±ΈΣ|x1-x2|Γ±Ϋβ¥πΘ§
¥Υ ±|x1-x2|=|y1-y2|Θ§Φ¥AC=ADΘ§
ΓΏC «÷±œΏy=![]() x+3…œΒΡ“ΜΗωΕ·ΒψΘ§ΒψDΒΡΉχ±ξ «Θ®0Θ§1Θ©Θ§
x+3…œΒΡ“ΜΗωΕ·ΒψΘ§ΒψDΒΡΉχ±ξ «Θ®0Θ§1Θ©Θ§
Γύ…ηΒψCΒΡΉχ±ξΈΣΘ®x0Θ§ ![]() x0+3Θ©Θ§
x0+3Θ©Θ§
Γύ-x0=![]() x0+2Θ§
x0+2Θ§
¥Υ ±Θ§x0=-![]() Θ§
Θ§
ΓύΒψC”κΒψDΒΡΓΑΖ«≥ΘΨύάκΓ±ΒΡΉν–Γ÷ΒΈΣΘΚ|x0|=![]() Θ§
Θ§
¥Υ ±CΘ®-![]() Θ§
Θ§ ![]() Θ©Θ°
Θ©Θ°


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫχ––Ή ‘¥ΒΡ‘Όάϊ”ΟΘ§―ß–ΘΉΦ±Η’κΕ‘Ωβ¥φΒΡΉά“ΈΫχ––Έ§–όΘ§œ÷”–ΦΉΓΔ““ΝΫΡΨΙΛΉιΘ§ΦΉΟΩΧλ–όΉάΒ 14 ΧΉΘ§““ΟΩΧλ±»ΦΉΕύ7ΧΉΘ§ΦΉΒΞΕά–όΆξ’β–©ΉάΒ ±»““ΒΞΕά–όΆξΕύ”Ο20ΧλΘ°―ß–ΘΟΩΧλΗΕΦΉΉι80‘Σ–όάμΖ―Θ§ΗΕ““Ήι120‘Σ–όάμΖ―Θ°
Θ®1Θ©«κΈ ―ß–ΘΩβ¥φΕύ…ΌΧΉΉάΒ ?
Θ®2Θ©‘Ύ–όάμΙΐ≥Χ÷–Θ§―ß–Θ“Σ≈…“ΜΟϊΙΛ»ΥΫχ––÷ ΝΩΦύΕΫΘ§―ß–ΘΗΚΒΘΥϊΟΩΧλ10‘Σ…ζΜν≤Ι÷ζΖ―Θ§œ÷”–»ΐ÷÷–όάμΖΫΑΗΘΚΔΌ”…ΦΉΒΞΕά–όάμΘΜΔΎ”…““ΒΞΕά–όάμΘΜΔέΦΉΓΔ““ΚœΉςΆ§ ±–όάμΘ°Ρψ―ΓΡΡ÷÷ΖΫΑΗΘ§ΈΣ ≤Ο¥?
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΥΒΖ®≤Μ’ΐ»ΖΒΡ «( )
A. 0Φ»≤Μ «’ΐ ΐΘ§“≤≤Μ «ΗΚ ΐ B. 1 «ΨχΕ‘÷ΒΉν–ΓΒΡ ΐ
C. ΜΞΈΣΒΙ ΐΒΡΝΫΗω ΐΒΡ≥ΥΜΐΈΣ1 D. 0ΒΡΨχΕ‘÷Β «0
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
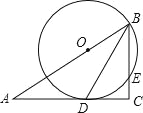
ΓΨΧβΡΩΓΩ(2016ΙψΈς ΓΡœΡΰ –ΒΎ21Χβ)‘ΎΆΦΓΑ ιœψΑΥΙπΘ§‘ΡΕΝ‘≤ΟΈΓ±ΕΝ ΐΜνΕ·÷–Θ§Ρ≥÷–―ß…η÷ΟΝΥ ιΖ®ΓΔΙζ―ßΓΔΥ–ΕΝΓΔ―ίΫ≤ΓΔ’ςΈΡΥΡΗω±»»ϋœνΡΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§BD «Ϋ«ΤΫΖ÷œΏΘ§ΒψO‘ΎAB…œΘ§“‘ΒψOΈΣ‘≤–ΡΘ§OBΈΣΑκΨΕΒΡ‘≤Ψ≠ΙΐΒψDΘ§ΫΜBC”ΎΒψEΘ°
Θ®1Θ©«σ÷ΛΘΚAC «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»τOB=10Θ§CD=8Θ§«σBEΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΓςABCΒΡ»ΐ±Ώ÷°±»ΈΣ2ΓΟ3ΓΟ4Θ§»τΓςDEF”κΓςABCœύΥΤΘ§«“ΓςDEFΒΡΉν¥σ±Ώ≥ΛΈΣ20Θ§‘ρΓςDEFΒΡ÷ή≥ΛΈΣ__________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΜΣΈΣ ÷Μζ”ΣœζΑ¥≈ζΝΩΆΕ»κ –≥ΓΘ§ΒΎ“Μ¥ΈΆΕΖ≈20000Χ®Θ§ΒΎ»ΐ¥ΈΆΕΖ≈80000Χ®Θ§ΟΩ¥ΈΑ¥œύΆ§ΒΡ‘ω≥Λ¬ ΆΕΖ≈Θ§…η‘ω≥Λ¬ ΈΣxΘ§‘ρΩ…Ν–ΖΫ≥ΧΘ® Θ©
A.20000Θ®1+xΘ©2=80000
B.20000Θ®1+xΘ©+20000Θ®1+xΘ©2=80000
C.20000Θ®1+x2Θ©=80000
D.20000+20000Θ®1+xΘ©+20000Θ®1+xΘ©2=80000
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΝ§Ϋ”»ΐΫ«–ΈΝΫ±Ώ÷–ΒψΒΡœΏΕΈΫ–Ήω»ΐΫ«–ΈΒΡ.»ΐΫ«–ΈΒΡ÷–ΈΜœΏΒΎ»ΐ±Ώ,«“Β»”ΎΒΎ»ΐ±ΏΒΡ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΙϊΫΪ≈ΉΈοœΏyΘΫ©¹2x2œρ”“ΤΫ“Τ3ΗωΒΞΈΜΘ§Ρ«Ο¥ΥυΒΟΒΫΒΡ–¬≈ΉΈοœΏΒΡΕ‘≥Τ÷α «÷±œΏ____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ(2016Κΰ±± ΓΨΘ÷ί –ΒΎ25Χβ)‘ΡΕΝΘΚΈ“Ο«‘ΦΕ®Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Ψ≠ΙΐΡ≥Βψ«“ΤΫ––”ΎΉχ±ξ÷αΜρΤΫ––”ΎΝΫΉχ±ξ÷αΦ–Ϋ«ΤΫΖ÷œΏΒΡ÷±œΏΘ§Ϋ–ΗΟΒψΒΡΓΑΧΊ’ςœΏΓ±Θ°άΐ»γΘ§ΒψMΘ®1Θ§3Θ©ΒΡΧΊ’ςœΏ”–ΘΚx=1Θ§y=3Θ§y=x+2Θ§y=©¹x+4Θ°
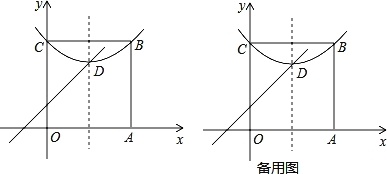
Έ Χβ”κΧΫΨΩΘΚ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–”–’ΐΖΫ–ΈOABCΘ§ΒψB‘ΎΒΎ“ΜœσœόΘ§AΓΔCΖ÷±π‘Ύx÷αΚΆy÷α…œΘ§≈ΉΈοœΏ![]() Ψ≠ΙΐBΓΔCΝΫΒψΘ§ΕΞΒψD‘Ύ’ΐΖΫ–ΈΡΎ≤ΩΘ°
Ψ≠ΙΐBΓΔCΝΫΒψΘ§ΕΞΒψD‘Ύ’ΐΖΫ–ΈΡΎ≤ΩΘ°
Θ®1Θ©÷±Ϋ”–¥≥ωΒψDΘ®mΘ§nΘ©Υυ”–ΒΡΧΊ’ςœΏΘΜ
Θ®2Θ©»τΒψD”–“ΜΧθΧΊ’ςœΏ «y=x+1Θ§«σ¥Υ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©ΒψP «AB±Ώ…œ≥ΐΒψAΆβΒΡ»Έ“β“ΜΒψΘ§Ν§Ϋ”OPΘ§ΫΪΓςOAP―ΊΉ≈OP’έΒΰΘ§ΒψA¬δ‘ΎΒψAΓδΒΡΈΜ÷ΟΘ§Β±ΒψAΓδ‘ΎΤΫ––”ΎΉχ±ξ÷αΒΡDΒψΒΡΧΊ’ςœΏ…œ ±Θ§¬ζΉψΘ®2Θ©÷–ΧθΦΰΒΡ≈ΉΈοœΏœρœ¬ΤΫ“ΤΕύ…ΌΨύάκΘ§ΤδΕΞΒψ¬δ‘ΎOP…œΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com