
【题目】(2016湖北省荆州市第25题)阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.
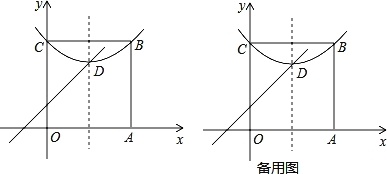
问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
【答案】(1)、x=m,y=n,y=x+n﹣m,y=﹣x+m+n;(2)、y=![]() (x﹣2)2+3;(3)、
(x﹣2)2+3;(3)、![]() 或
或![]()
【解析】
试题分析:(1)、根据特征线直接求出点D的特征线;(2)、由点D的一条特征线和正方形的性质求出点D的坐标,从而求出抛物线解析式;(3)、分平行于x轴和y轴两种情况,由折叠的性质计算即可.
试题解析:(1)、∵点D(m,n), ∴点D(m,n)的特征线是x=m,y=n,y=x+n﹣m,y=﹣x+m+n;
(2)、点D有一条特征线是y=x+1, ∴n﹣m=1, ∴n=m+1
∵抛物线解析式为![]() , ∴y=
, ∴y=![]() (x﹣m)2+m+1,
(x﹣m)2+m+1,
∵四边形OABC是正方形,且D点为正方形的对称轴,D(m,n), ∴B(2m,2m),
∴![]() (2m﹣m)2+n=2m,将n=m+1带入得到m=2,n=3; ∴D(2,3), ∴抛物线解析式为y=
(2m﹣m)2+n=2m,将n=m+1带入得到m=2,n=3; ∴D(2,3), ∴抛物线解析式为y=![]() (x﹣2)2+3
(x﹣2)2+3
(3)、如图,当点A′在平行于y轴的D点的特征线时,
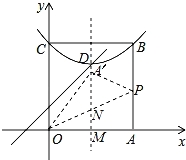
根据题意可得,D(2,3), ∴OA′=OA=4,OM=2, ∴∠A′OM=60°, ∴∠A′OP=∠AOP=30°,
∴MN=![]() =
=![]() , ∴抛物线需要向下平移的距离=3﹣
, ∴抛物线需要向下平移的距离=3﹣![]() =
=![]() .
.
当点A′在平行于x轴的D点的特征线时,
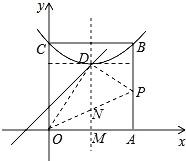
∵顶点落在OP上, ∴A′与D重合, ∴A′(2,3), 设P(4,c)(c>0),
由折叠有,PD=PA, ∴![]() =c, ∴c=
=c, ∴c=![]() , ∴P(4,
, ∴P(4,![]() ) ∴直线OP解析式为y=
) ∴直线OP解析式为y=![]() ,
,
∴N(2,![]() ), ∴抛物线需要向下平移的距离=3﹣
), ∴抛物线需要向下平移的距离=3﹣![]() =
=![]() ,
,
抛物线向下平移![]() 或
或![]() 距离,其顶点落在OP上.
距离,其顶点落在OP上.
考点(1)、折叠的性质;(2)、正方形的性质;(3)、特征线的理解


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() 与
与![]() 的“非常距离”给出下列定义: 若
的“非常距离”给出下列定义: 若![]() ,则点
,则点![]() 与
与![]() 的“非常距离”为
的“非常距离”为![]() ;
;
若![]() ,则点
,则点![]() 与
与![]() 的“非常距离”为
的“非常距离”为![]() . 例如:点
. 例如:点![]() ,点
,点![]() ,因为
,因为![]() ,所以点
,所以点![]() 与
与![]() 的“非常距离”为
的“非常距离”为![]() ,也就是图1中线段
,也就是图1中线段![]() 与线段
与线段![]() 长度的较大值(点Q为垂直于
长度的较大值(点Q为垂直于![]() 轴的直线
轴的直线![]() 与垂直于
与垂直于![]() 轴的直线
轴的直线![]() 的交点).
的交点).
(1)已知点A![]() ,B为
,B为![]() 轴上一个动点.
轴上一个动点.
①若点B(0,3),则点A与点B的“非常距离”为 ;
②若点A与点B的“非常距离”为2,则点B的坐标为 ;
③直接写出点A与点B的“非常距离”的最小值 .
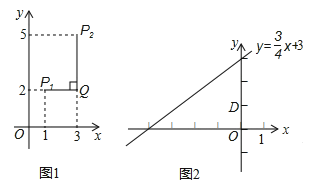
(2)已知点D(0,1)点C是直线![]() 上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016贵州省毕节市第23题)为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。
(1)、求这两年该县投入教育经费的年平均增长率;
(2)、若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2﹣6x=3,配方正确的是( )
A. (x﹣3)2=0 B. (x﹣3)2=6 C. (x﹣3)2=9 D. (x﹣3)2=12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com