
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.

【答案】(1)证明见解析;(2) 2cm.
【解析】试题分析:(1)根据同角的余角相等可得∠BCE=∠CAD,再由全等三角形的判定定理AAS即可判定△ADC≌△CEB;(2)利用(1)中的全等三角形的对应边相等得到:AD=CE=5cm,CD=BE.则根据图中相关线段的和差关系得到BE=AD-DE,即可求得BE的长度.
试题解析:(1)证明:如图,∵AD⊥CE,∠ACB=90°,
∴∠ADC=∠ACB=90°,
∴∠BCE=∠CAD(同角的余角相等).
在△ADC与△CEB中,
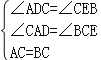 ,
,
∴△ADC≌△CEB(AAS);
(2)由(1)知,△ADC≌△CEB,则AD=CE=5cm,CD=BE.
如图,∵CD=CE﹣DE,
∴BE=AD﹣DE=5﹣3=2(cm),即BE的长度是2cm.


科目:初中数学 来源: 题型:
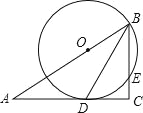
【题目】(2016广西省南宁市第21题)在图“书香八桂,阅读圆梦”读数活动中,某中学设置了书法、国学、诵读、演讲、征文四个比赛项目如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
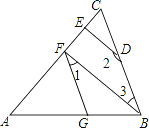
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用因式分解法解一元二次方程x(x﹣3)=x﹣3时,原方程可化为( )
A.(x﹣1)(x﹣3)=0
B.(x+1)(x﹣3)=0
C.x (x﹣3)=0
D.(x﹣2)(x﹣3)=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖北省荆州市第25题)阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.
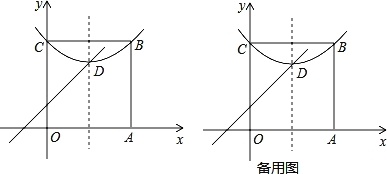
问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
查看答案和解析>>
科目:初中数学 来源: 题型:
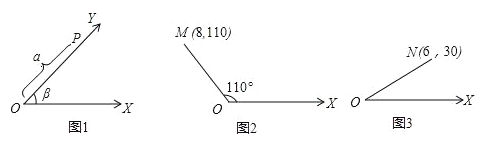
【题目】如图1,将射线OX按逆时针方向旋转β角,得到射线OY,如果点P为射线OY上的一点,且OP=a,那么我们规定用(a,β)表示点P在平面内的位置,并记为P(a,β),例如,图2中,如果OM=8,∠XOM=110°,那么点M在平面内的位置,记为M(8,110),根据图形,解答下面的问题:
(1)如图3,如果点N在平面内的位置记为N(6,30),那么ON= ;∠XON= .
(2)如果点A、B在平面内的位置分别记为A(5,30),B(12,120),试求A、B两点之间的距离并画出图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com