
 如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).求:
如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).求:分析 (1)根据待定系数法即可解决.
(2)分两种情形讨论,添加辅助线构造全等三角形即可求出点D坐标.
(3)分OP=OC、CP=CO、PC=PO三种情形研究即可.
解答 解:(1)∵正比例函数y=kx的图象经过点C(3,4),
∴4=3k,
k=$\frac{4}{3}$,
∵一次函数y=k1x+b的图象经过A(-3,0),C(3,4)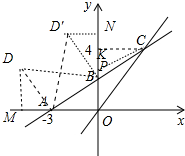
∴$\left\{\begin{array}{l}{-3k+b=0}\\{3k+b=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=2}\end{array}\right.$,
∴一次函数为y=$\frac{2}{3}x+2$.
(2)①当DA⊥AB时,作DM⊥x轴垂足为M,
∵∠DAM+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠DAM=∠ABO,
∵DA=AB,∠DMA=∠AOB,
∴△DAM≌△ABO,
∴DM=AO=3,AM=BO=2,
∴D(-5,3),
②当D′B⊥AB时,作D′N⊥y轴垂足为N,
同理得△D′BN≌△BAO
∴D′N=BO=2,BN=AO=3,
∴D′(-2,5)
∴D点坐标为(-5,3)或(-2,5).
(3)当OP=OC时,OC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
则P的坐标为(0,5)或(0,-5),
当CP=CO时,则P的坐标是(0,8),
当PO=PC时,作CK⊥y轴垂足为K,设P的坐标为,(0,t)
在Rt△PCK中,∵PC=t,PK=4-t,KC=3,
∴(4-t)2+32=t2解得$t=\frac{25}{8}$
此时P的坐标是$(0,\frac{25}{8})$
综上可知P的坐标为(0,5)或(0,-5)或(0,8)或$(0,\frac{25}{8})$.
点评 本题考查待定系数法求一次函数、全等三角形的判定和性质、勾股定理、添加辅助线构造全等三角形等知识,学会分类讨论的数学思想是正确解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $2\sqrt{2}-1$ | B. | $2\sqrt{2}-2$ | C. | $2-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠BAC=90°,取BF=AB,作DF⊥BC交AC于D,作AE⊥BC于E.
如图,△ABC中,∠BAC=90°,取BF=AB,作DF⊥BC交AC于D,作AE⊥BC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com