
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.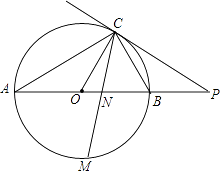
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MNMC的值.
【答案】
(1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB
AB
(3)解:连接MA,MB,
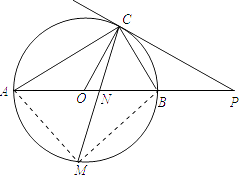
∵点M是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ![]() =
= ![]() .
.
∴BM2=MNMC.
又∵AB是⊙O的直径, ![]() =
= ![]() ,
,
∴∠AMB=90°,AM=BM.
∵AB=8,
∴BM=4 ![]() .
.
∴MNMC=BM2=32.
【解析】(1)利用直径上的圆周角是直角和圆的定义易证;
(2)利用等腰三角形的性质和直角三角形的性质来证明;
(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,从而可证得△MBN∽△MCB.再利用相似三角形的对应边成比例得到BM2=MNMC.在Rt△ABM中求出BM,即可得到结论.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】若我们规定三角“![]() ”表示为:abc;方框“
”表示为:abc;方框“![]() ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如:![]() =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
(1)计算:![]() = ______ ;
= ______ ;
(2)代数式 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;
(3)解方程:![]() =6x2+7.
=6x2+7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=![]() 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
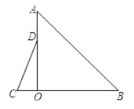
【题目】如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,己知A(6,0),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),点C的坐标为
中,己知A(6,0),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),点C的坐标为![]() ,且
,且![]() 连接OC,AB,CD,BD.
连接OC,AB,CD,BD.
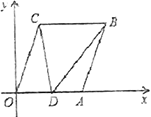
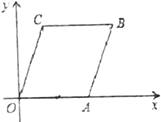
(1)写出点C的坐标为______;点B的坐标为________;
(2)当![]() 的面积是
的面积是![]() 的面积的3倍时,求点D的坐标;
的面积的3倍时,求点D的坐标;
(3)设![]() ,
,![]() ,
,![]() ,判断
,判断![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答下面的问题:
我们知道方程![]() 有无数个解,但在实际问题中往往只需求出其正整数解.
有无数个解,但在实际问题中往往只需求出其正整数解.
例:由![]() ,得:
,得:![]() (
( ![]() 、
、![]() 为正整数).要使
为正整数).要使![]() 为正整数,则
为正整数,则![]() 为正整数,可知:
为正整数,可知: ![]() 为3的倍数,从而
为3的倍数,从而![]() ,代入
,代入![]() .所以
.所以![]() 的正整数解为
的正整数解为![]() .
.
问题:
(1)请你直接写出方程![]() =8的正整数解 .
=8的正整数解 .
(2)若![]() 为自然数,则满足条件的正整数
为自然数,则满足条件的正整数![]() 的值有( )
的值有( )
A.3个 B.4个 C.5个 D.6个
(3)关于![]() ,
, ![]() 的二元一次方程组
的二元一次方程组![]() 的解是正整数,求整数
的解是正整数,求整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.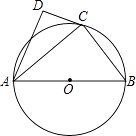
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com