
 与
与 ,
, 与
与 .
.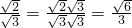 .
.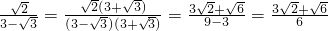 .
.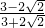 ;②
;②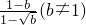 ;
;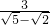 时,甲的解法是:
时,甲的解法是: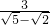 =
= =
=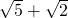 ,乙的解法是:
,乙的解法是: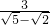 =
=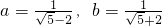 =
=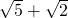 ,以下判断正确的是
,以下判断正确的是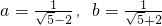 ,则
,则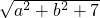 的值为
的值为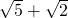 与
与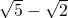 ,答案不唯一;
,答案不唯一;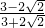 =
=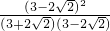 =17-12
=17-12 ;
;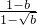 =
=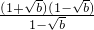 =1+
=1+ ;
; =
=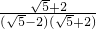 =
= +2
+2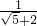 =
= =
= -2
-2 +2)2+(
+2)2+( -2)2=18
-2)2=18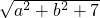 =
=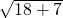 =5.故选A.
=5.故选A.

科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解



 B、
B、 C、
C、


查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| a |
| a |
| 2 |
| 2 |
| ||
|
| ||||
|
| ||
| 3 |
| ||
3-
|
| ||||
(3-
|
3
| ||||
| 9-3 |
3
| ||||
| 6 |
3-2
| ||
3+2
|
| 1-b | ||
1-
|
| 3 | ||||
|
| 3 | ||||
|
3(
| ||||||||
(
|
| 5 |
| 2 |
| 3 | ||||
|
(
| ||||||||
|
| 5 |
| 2 |
| 1 | ||
|
| 1 | ||
|
| a2+b2+7 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源:2011-2012学年黑龙江虎林850农场学校八年级下学期期中数学试卷(带解析) 题型:解答题
先阅读下面的材料,然后解答问题:通过观察,发现方程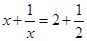 的解为
的解为 ;
; 的解为
的解为 ;
; 的解为
的解为 ;
;
…………………………
【小题1】观察上述方程的解,猜想关于x的方程 的解是________________;
的解是________________;
【小题2】根据上面的规律,猜想关于x的方程 的解是___________________;
的解是___________________;
【小题3】把关于x的方程 变形为方程
变形为方程 的形式
的形式
是______ _ _,方程的解是________ ___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com